How do you find the equation of a circle with points (1, 2) and (–1, –2) as endpoints of a diameter?

Question

8393 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2016-11-25T06:47:26

#x^2+y^2=5#

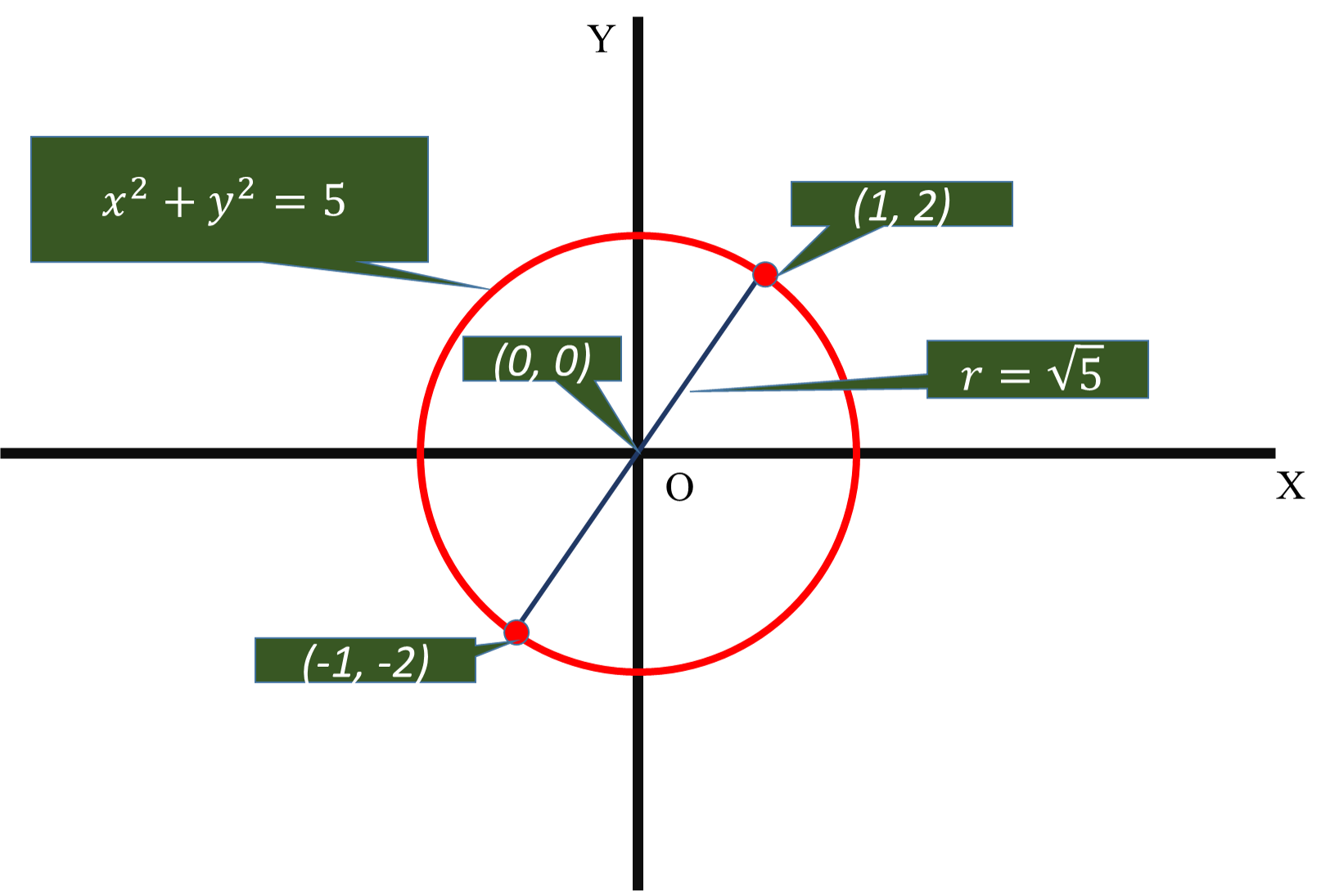
Refer the image

The circle is passing through the points #(-1, -2) and (1, 2)#

This is the diameter of the circle. Its midpoint is the center of the circle and half of the diameter is the radius of the circle.

Mid - point / center of the circle

#(x, y)= (x_1+x_2)/2, (y_1+y_2)/2#
#(x, y)= (-1+1)/2, (-2+2)/2 = (0, 0)#

Center of the circle is #(0, 0)#

Its radius is the distance between #(0, 0)# and #(1, 2)#

#r=sqrt[(x_1-x_2)+(y_1-y_2)]#
#r=sqrt[(0-(-1))+(0-(-2))#
#r=sqrt(1+4)=sqrt5#

The equation of the circle having #(0, 0)# as the center is -

#x^2+y^2=r^2#

in our case -

#r=sqrt5#
Then -
#r=5#

Hence the required equation is -

#x^2+y^2=5#