Question

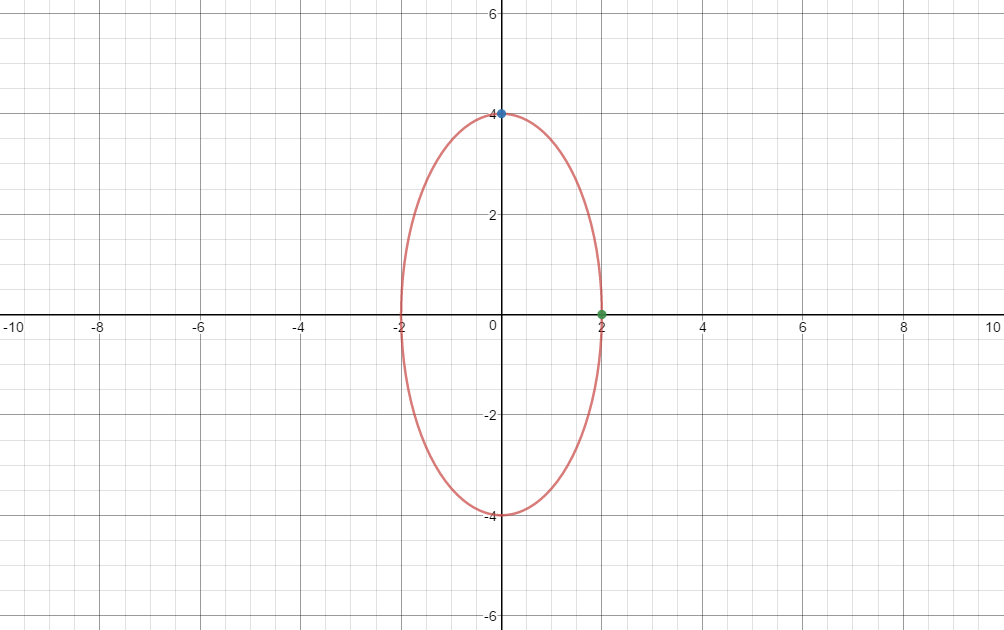
How do you find the equation of an ellipse with major axis vertical and passes through points (0,4) and (2,0)?

Answer 1

This problem can only be done, if one assumes that two given points, `(0,4) and (2,0)`, are the upper vertex on major axis and right vertex on the minor axis, respectively.

Explanation:

The general Cartesian equation for an ellipse with a vertical major axis is:

`(y - k)^2/a^2 + (x - h)^2/b^2 = 1" [1]"`

Where x and y correspond any point, `(x, y)` in the ellipse, h and k correspond to the center point `(h, k)`, "a" is the length of the semi-major axis, and "b" is the length of the semi-minor axis.

Using the previously stated assumption.

The upper vertex on the major axis will have the coordinates:

`(h, k + a)`

The right vertex on the minor axis will have the coordinates:

`(h + b, k)`

Matching these two point to the given points:

`(h, k + a) = (0,4)`
`(h + b, k) = (2,0)`

This allows us to write the following equations:

`h = 0, k + a = 4, h + b = 2, and k = 0`

Substituting 0 for h and k:

`h = 0, a = 4, b = 2, and k = 0`

Substitute these 4 values into equation [1]:

`(y - 0)^2/4^2 + (x - 0)^2/2^2 = 1" [2]"`

Equation [2] is the answer.

Here is a graph with the ellipse and the two points plotted: