How do you find the equation of an ellipse with vertices #(0,+-5)# and passes through the point (4,2)?
1 Answer
Because the vertices are vertically oriented, we use the general Cartesian form:
where
Explanation:
The general form for vertically oriented vertices are:
These general forms and the given vertices
Substitute these values into equation [1]:
Substitute the point
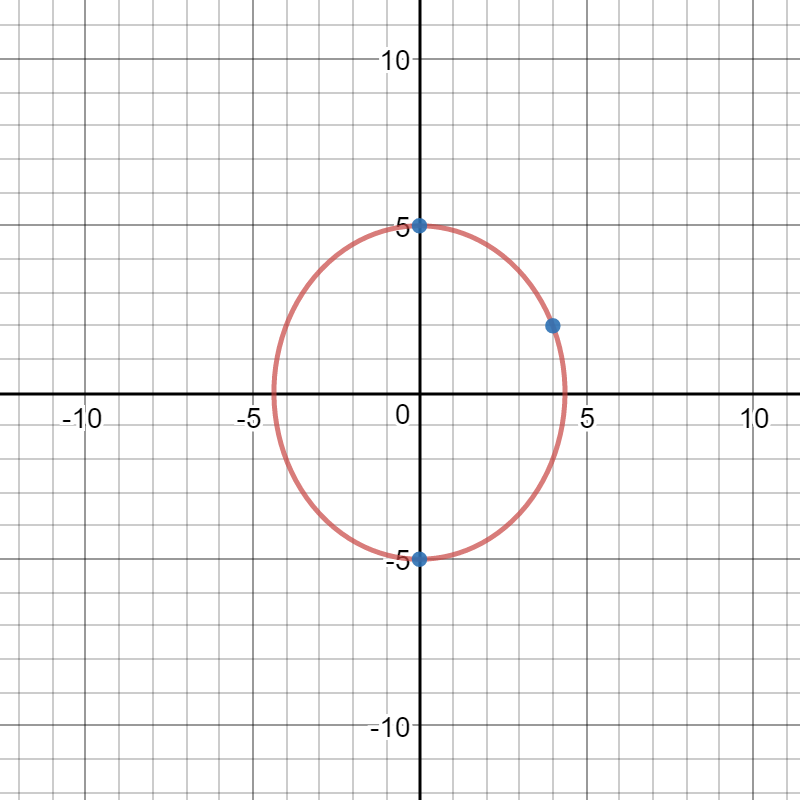
Here is a graph of equation [3] and the three points: