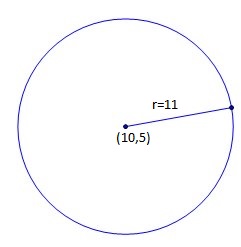
How do you find the equation of the circle given center at the (10, 5) and a radius of 11?
2 Answers
Mar 20, 2018
Explanation:
#"the standard form of the equation of a circle is"#
#color(red)(bar(ul(|color(white)(2/2)color(black)((x-a)^2+(y-b)^2=r^2)color(white)(2/2)|)))#
#"where "(a,b)" are the coordinates of the centre and r is"#
#"the radius"#
#"here "(a,b)=(10,5)" and "r=11#
#rArr(x-10)^2+(y-5)^2=121larrcolor(red)"equation of circle"#
Mar 20, 2018
Explanation:
To find the equation of a circle whose radius and center has been given, we have a formula,
where,
So,
Hope this helps :)

