Question

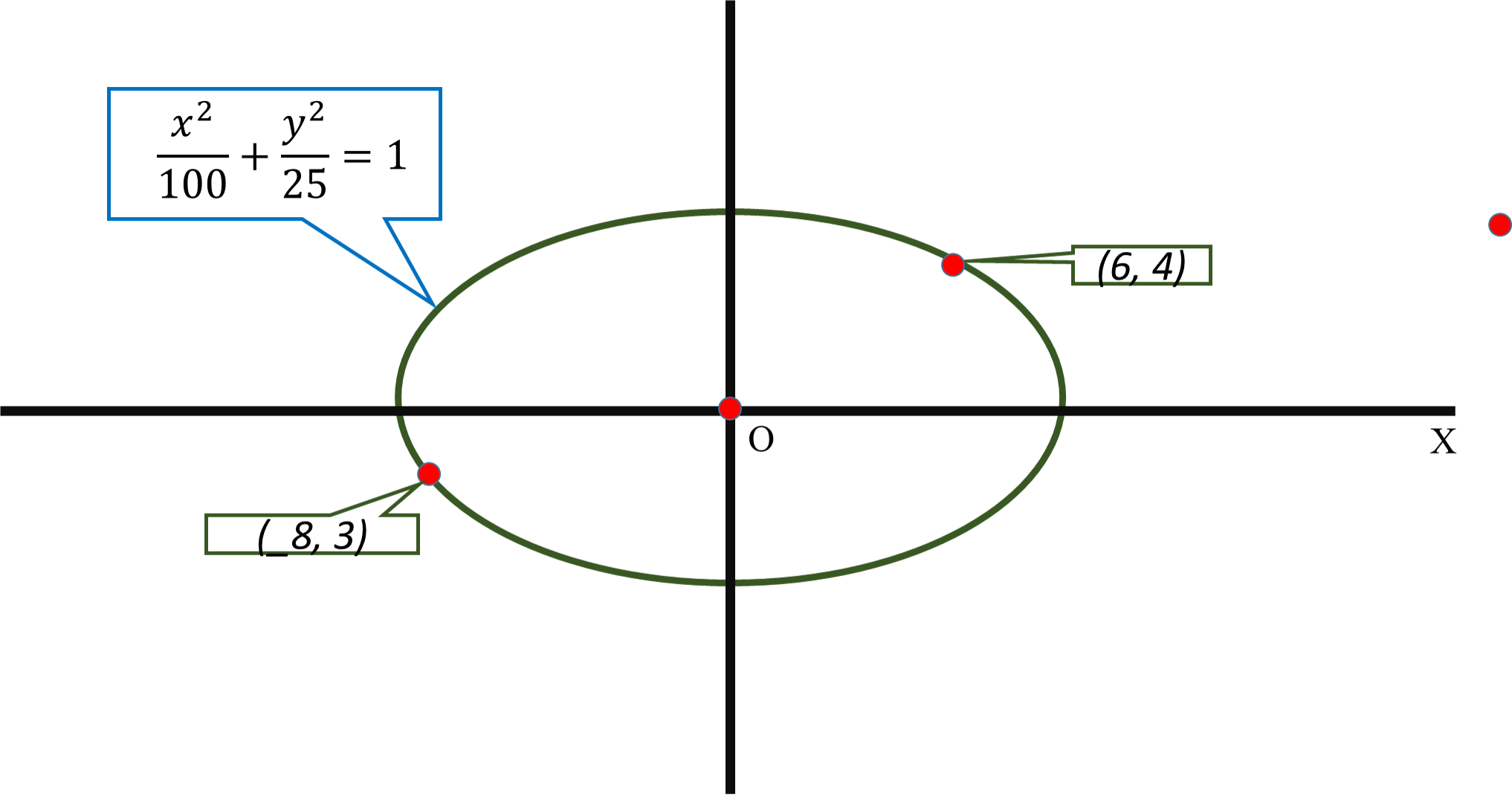
How do you find the equation of the ellipse that passes through points (6,4) and (-8,3) ?

Answer 1

`x^2/100+y^2/25=1`

Explanation:

Two Points are given. The center is not given.
We shall take `(0, 0)` as the center.

The equation of the ellipse is -

`(x-h)^2/a^2+(y-k)^2/b^2=1`

Plug in the values of center

`(x-0)^2/a^2+(y-0)^2/b^2=1`

This is the equation of the ellipse having center as`(0, 0)`

`x^2/a^2+y^2/b^2=1`

The given ellipse passes through points `(6, 4); (-8, 3)`

First plugin the values `(6, 4)`

`6^2/a^2+4^2/b^2=1`
`36/a^2+16/b^2=1` ------------(1)

Next Plugin the values `(-8, 3)`

`(-8)^2/a^2+3^2/b^2=1`
`64/a^2+9/b^2=1` -----------------(2)

`36/a^2+16/b^2=1` ------------(1)
`64/a^2+9/b^2=1` -----------------(2)

We shall rewrite the equations as -

`36 1/a^2+16 1/b^2=1` ------------(1)
`64 1/a^2+9 1/b^2=1` -----------------(2)

Let `1/a^2=m ; 1/b^2=n`

Then these two equations become

`36m+16n =1` ------------(1)
`64m+9n=1` -----------------(2)

Now we can easily solve

`36m+16n =1` ------------(1) `xx9`
`64m+9n=1` -----------------(2)`xx16`

`324m+144n =9` ------------(1)
`1024m+144n=16` -----------------(2)

Subtract (2) from (1)

`-700m=-7`
`m=(-7)/(-700)=1/100`

Plugin this in any one of the euations

`36 * 1/100+16n =1`

`16n=1-36/100=(100-36)/100=16/25`
`n=16/25*1/16=1/25`

`m=1/a^2=1/100`
`n=1/b^2=1/25`

`x^2/a^2+y^2/b^2=1`

This equation can also be written as -

`1/a^2*x^2+1/b^2*y^2=1`

Now you can easily plugin the values of `1/a^2 ; 1/b^2`

`1/100*x^2+1/25*y^2=1`

`x^2/100+y^2/25=1`