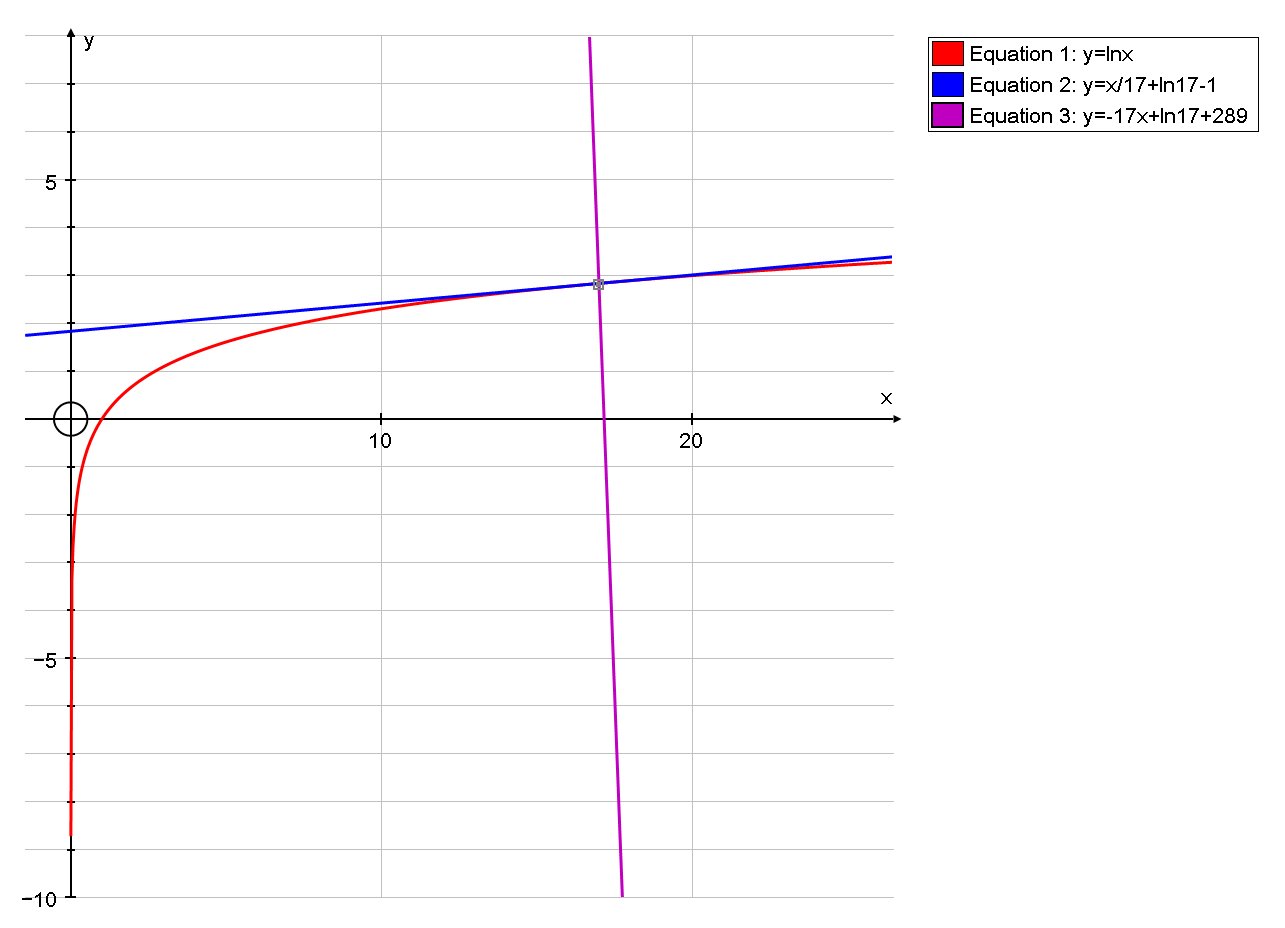
How do you find the equation of the tangent and normal line to the curve #y=lnx# at x=17?
1 Answer
Nov 2, 2016
Tangent Equation :
Normal Equation :
Explanation:
If
When
so the tangent passes through
Using
The normal is perpendicular to the tangent, so the product of their gradients is -1 hence normal passes through
so the equation of the normal is: