The equation of the tangent line is composed of two parts: the derivative (slope), and the #y#-intercept. The problem contains all the information necessary to solve it; we just have to be clever and use the right techniques.
First we find the derivative of our function at #x=3#. This will be the slope of the tangent line. (The tangent line is straight, so the slope is the same at all points - whether it's #x=3, 4, 5, 6, 7,#etc). The derivative of the natural log function is #1/x#, so we know the derivative of #ln(3x-5)# will be #1/(3x-5)#.
However, the chain rule tells us that we need to multiply this by the derivative of the "inside" function (in our case, #3x-5#) - which is #3#. Therefore, the complete derivative is
#y'(x)=3/(3x-5)#.
To find the derivative at #x=3#, we simply plug in #3# for #x#:
#y'(3)=3/(3(3)-5)#
#y'(3)=3/(9-5)#
#y'(3)=3/4#
Thus the slope of our tangent line is #3/4#. Now, finding the #y#-intercept requires the slope - which we have - and a point from the function #y=ln(3x-5)#. Because we're evaluating the tangent line at #x=3#, we will use #3# to find our point:
#y(3)=ln(3(3)-5)#
#y(3)=ln(9-5)#
#y(3)=ln(4)#
We can finally move on to the last step - finding the actual equation. Because we know the tangent line is straight, it will be of the form #y=mx+b#, where #m# is the slope and #b# is the #y#-intercept. We have everything we need:
#y=ln(4)-># (#y# part of the point)
#x=3-># (#x# part of the point)
#m=3/4-># (slope)
Let's plug these numbers into our equation:
#ln(4)=(3/4)(3)+b#
#ln(4)=9/4+b#
#ln(4)-9/4=b#
That's our #y#-intercept, making the equation of the tangent line #y=3/4x+ln(4)-9/4#. If you prefer hard numbers instead of logs and fractions, this can be approximated to
#y=3/4x-.864#
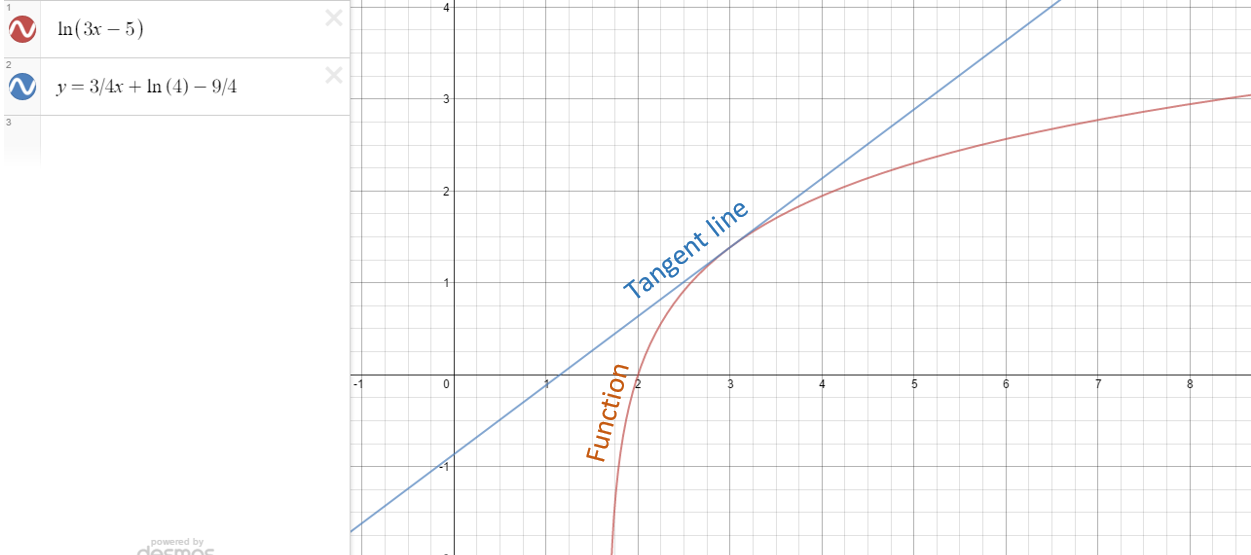
See the graph below for a visual description of the solution.