How do you find the equations for the tangent plane to the surface #xy^2+3x-z^2=4# through #(2, 1, -2)#?
1 Answer
Explanation:
1) rearrange eqn to
so:
2) find normal by calculating
remember when partially differentiating: differentiate with respect to the variable in question, treating the other variables as constant.
now evaluate this at
3) the eqn of a plane in vector form is
#vecr * vecn=((x_1),(y_1),(z_1)) * vecn#
where
so:
#((x),(y),(z)) * ((4),(4),(4))=((2),(1),(-2)) * ((4),(4),(4))#
# :. 4x+4y+4z=8+4-8#
# :. 4x+4y+4z=4#
# :. x+y+z=1#
We can confirm this result graphically:
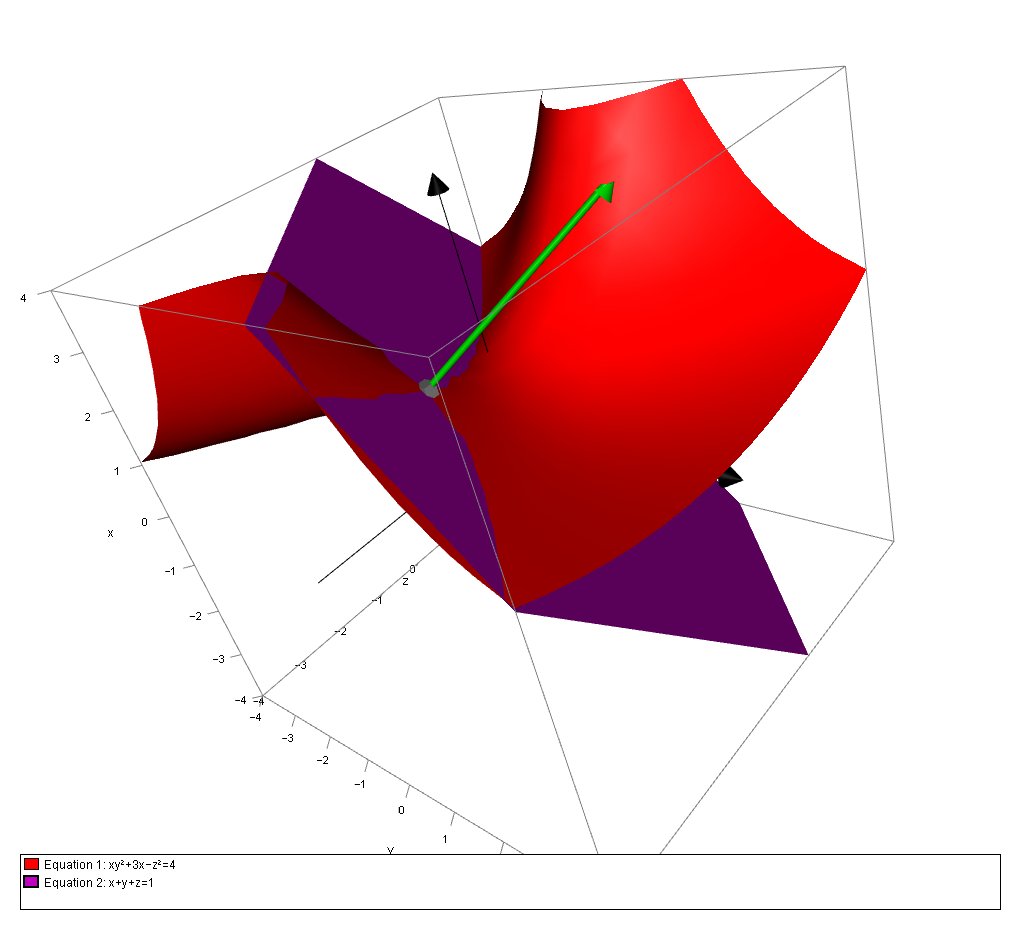 #
#


