Question

How do you find the exact functional value sin (pi/12) using the cosine sum or difference identity?

Answer 1

`color(red)(cos(π/12) = (1+ sqrt3)/(2sqrt2))`

Explanation:

`cos(π/12)= cos((3π)/12-(2π)/12) = cos (π/4-π/6)`

The cosine difference identity is:

`cos(A-B) = cosAcosB+sinAsinB`

∴ `cos(π/12) = cos(π/4)cos(π/6) + sin(π/4)sin(π/6)`

We can use the unit circle to work out the values.

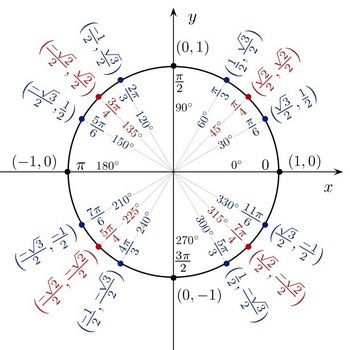
(from www.algebra.com)

`cos(π/12) =cos(π/4)cos(π/6) + sin(π/4)sin(π/6) = sqrt2/2×sqrt3/2 + sqrt 2/2×1/2`

`cos(π/12)= sqrt2/4(sqrt3+1)`

`cos(π/12) = (1+ sqrt3)/(2sqrt2)`

Answer 2

Find `sin (pi/12)`

Ans: `(sqrt(2 - sqrt3))/2`

Explanation:

Call `sin (pi/12) = sin t`
`cos 2t = cos ((2pi)/12) = cos ((pi)/6) = sqrt3/2`
Apply the trig identity: `cos 2t = 1 - sin^2 t`
`cos 2t = sqrt3/2 = 1 - 2sin^2 t`
`2sin^2 t = 1 - sqrt3/2 = (2 - sqrt3)/2`
`sin^2 t = (2 - sqrt3)/4`
`sin t = +- (sqrt(2 - sqrt3)/2)`
Since sin (pi/12) is positive (Quadrant I), then

`sin (pi/12) = sin t = sqrt ((2 - sqrt3))/2`

Check by calculator: `sin (pi/12) = sin 15 = 0.26`

`(sqrt(2 - sqrt3))/2 = sqrt2.68/2 = 0.517/2 = 0.26. OK`