Question

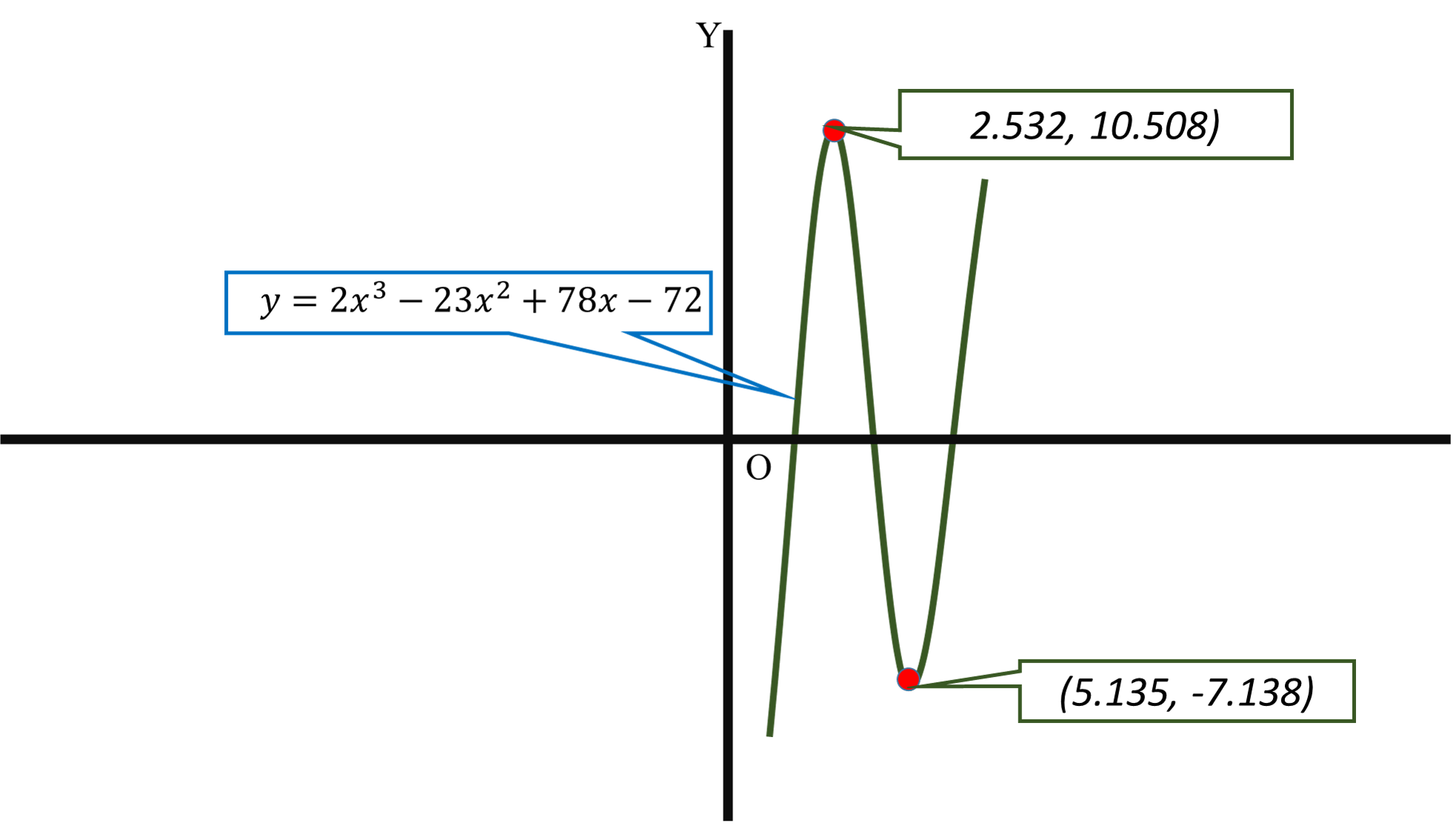
How do you find the exact relative maximum and minimum of the polynomial function of `2x^3 -23x^2+78x-72`?

Answer 1

There is a minimum at `x=5.135`
There is a maximum at `x=2.531`

Explanation:

Given -

`y=2x^3-23x^2+78x-72`

`dy/dx=6x^2-46x+78`

`(d^2y)/(dx^2)=12x-46`

`dy/dx=0 => 6x^2-46x+78=0`

`x=(-b+-sqrt(b^2 -4ac))/(2xxa)`

`x=(-(-46)+-sqrt((-46^2) -(4xx6xx78)))/(2xx6)`

`x=(46+-sqrt(2116-1872))/(2xx6)`

`x=(46+-sqrt(244))/(12)`

`x=(46+-15.62)/(12)`

`x=(46+15.62)/(12)=61.62/12=5.135`

`x=(46-15.62)/(12)=30.38/12=2.531`

At `x=5.135`

`(d^2y)/(dx^2)=12(5.135)-46=61.62-46=15.62 >0`

There is a minimum at `x=5.135`

At `x=2.531`

`(d^2y)/(dx^2)=12(2.531)-46=30.37-46=-15.628<0`

There is a maximum at `x=2.531`