Question

How do you find the exact value of `12(sin150)(cos150)`?

Answer 1

`sin 150 = sin((5pi)/6) = 1/2`
`cos 150 = cos((5pi)/6) = -(sqrt(3))/2`

`12*1/2*(-(sqrt(3))/2)=-3sqrt(3)`

Explanation:

You have to know the three basic "magic" numbers of sin and cos goniometric functions. They are: `1/2`, `sqrt(2)/2`, `sqrt(3)/2`.

Also calculating with radians may help you.
You know that `1pi` rad equals 180°.

Here is the unit circle, where you can find all sin and cos values for the basic angles.

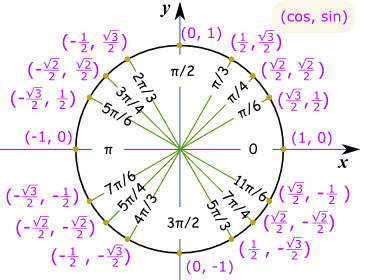
I used an image from this page:
https://www.mathsisfun.com [online]. [cit. 2016-11-27]. Available from: https://www.mathsisfun.com/geometry/unit-circle.html