How do you find the exact value of #tan300#?
2 Answers
Nov 9, 2016
Explanation:
A
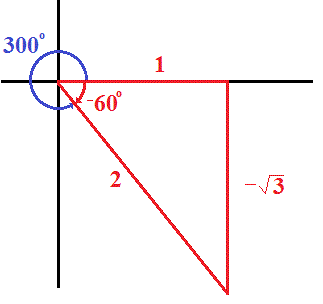
Nov 9, 2016
Explanation:
Now
Finally

