Question

How do you find the exact value of the six trigonometric functions of pi/4 radians?

Answer 1

`sin(pi/4) = sqrt2/2`
`cos(pi/4) = sqrt2/2`
`tan(pi/4) = 1`

`csc(pi/4) = sqrt2`
`sec(pi/4) = sqrt2`
`cot(pi/4) = 1`

Explanation:

`pi/4` radians is the same as 90 degrees. So, first draw a right triangle with an angle of `pi/4`:

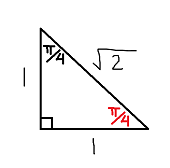
This creates a 45-45-90 triangle, also known as a right isosceles triangle. This is a very special triangle, and we know that both of its legs will be the same length, and the hypotenuse will be the length of one of the legs times `sqrt2`.

To make things easier for us, we will say the legs are both 1, and the hypotenuse, therefore, is `sqrt2`.

Now that we have a triangle with our 3 sides labeled (and our angle in red), we can find all 6 trig functions:

`sin(pi/4) = "opposite"/"hypotenuse" = 1/sqrt2 = sqrt2/2`

`cos(pi/4) = "adjacent"/"hypotenuse" = 1/sqrt2 = sqrt2/2`

`tan(pi/4) = "opposite"/"adjacent" = 1/1 = 1`

Now, the other three functions are just the inverses of the first three. Cosecant is the inverse of sine, secant is the inverse of cosine, and cotangent is the inverse of tangent. To see what I mean, look at this:

`csc(pi/4) = "hypotenuse"/"opposite" = sqrt2/1 = sqrt2`

`sec(pi/4) = "hypotenuse"/"adjacent" = sqrt2/1 = sqrt2`

`cot(pi/4) = "adjacent"/"opposite" = 1/1 = 1`

So there you have it! All 6 trig functions can be evaluated this way just by drawing a triangle and knowing its side lengths.

Final Answer