How do you find the foci and sketch the hyperbola #4y^2-4x^2=1#?
2 Answers
Please see the explanation.
Explanation:
The standard form for the equation of a hyperbola with a vertical transverse axis is:
The foci are located at the points:
Let's write your equation in the form of equation [1]:
Substituting into the patterns for the foci:
The foci are at the points:
Here is the graph with the foci:
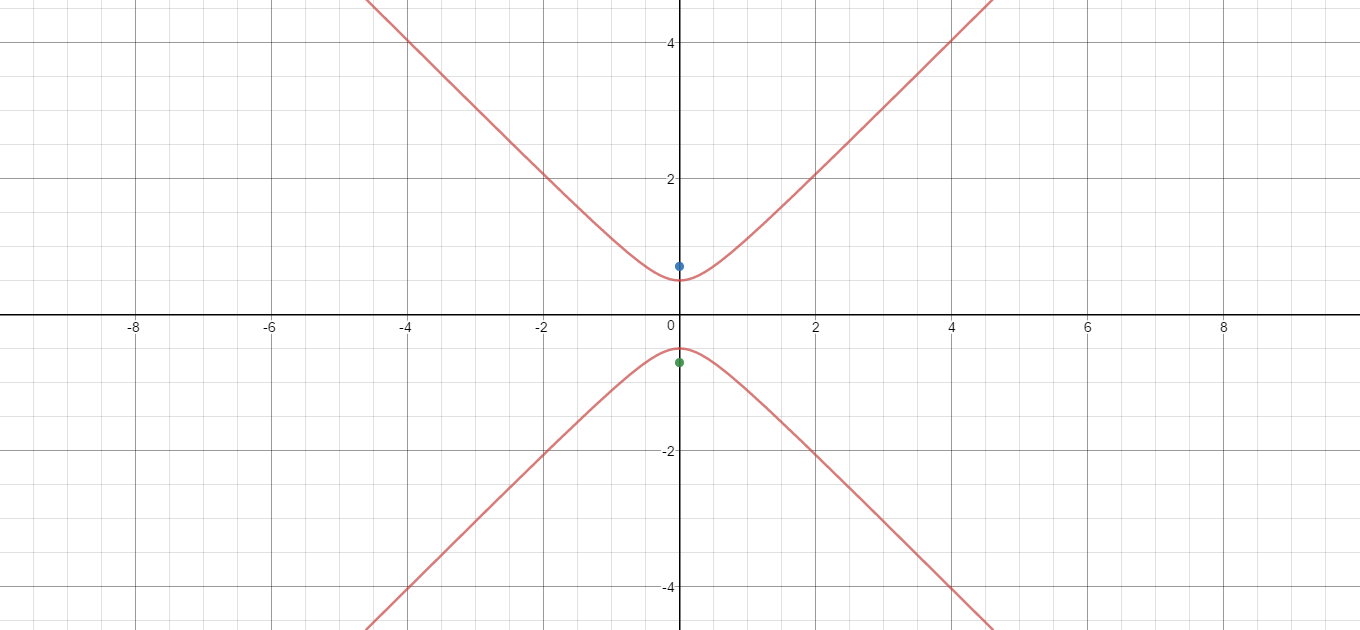
Foci :
Explanation:
graph{(4y^2-4x^2-1)(x^2-y^2)(x^2+(y-0.707)^2-.001)(x^2+(y+0.707)^2-.001)=0 [-2.5, 2.5, -1.25, 1.25]}
In the standard form,
rectangular ( RH ), with [asymptotes]
(https://socratic.org/precalculus/functions-defined-and-notation/asymptotes)
meeting at the center C(0, 0).
The semi axes
The eccentricity e of the RH is
The Vertices A and A' are
on the ( major ) axis, x = 0.
The foci S and S' on the major y- axis are
The directrixes DY, DY' are
Now, the RH can be sketched in the order
(i)the guide lines asymptotes
(ii) vertices
(iii) a few points like
