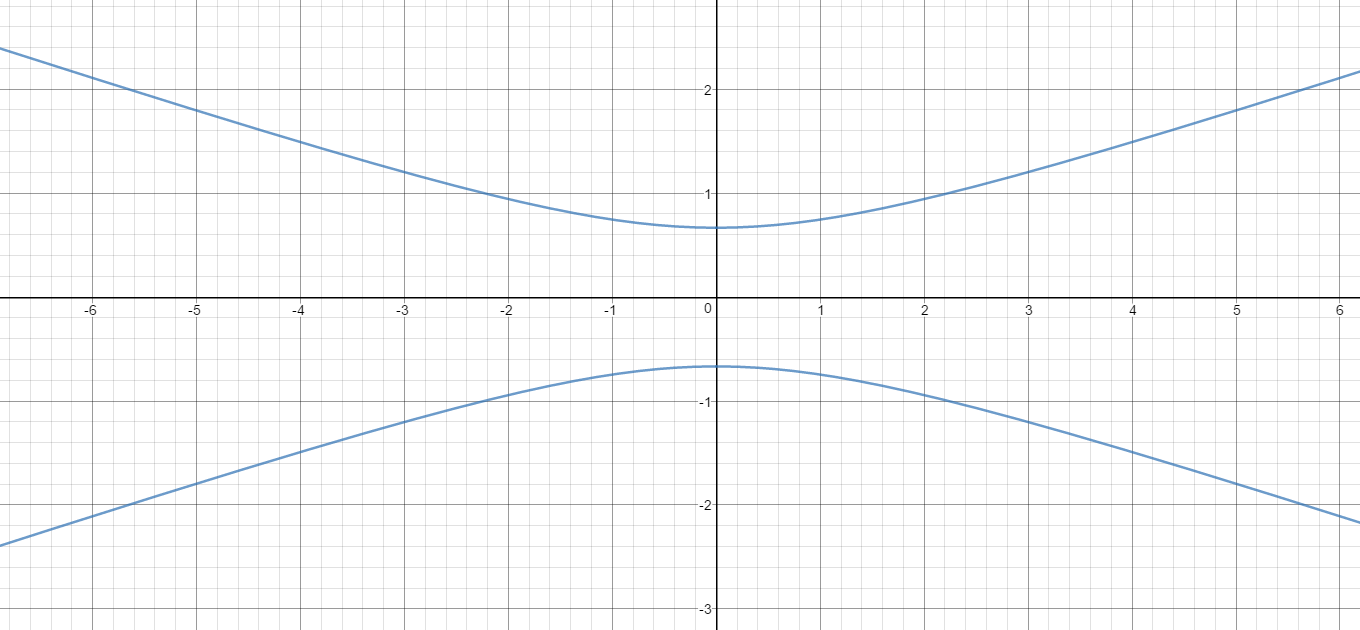
How do you find the foci and sketch the hyperbola #9y^2-x^2=4#?
1 Answer
Please read the explanation.
Explanation:
The standard form for a hyperbola of this type is:
where, x and y correspond to any point
Given:
We will be using algebraic steps to put the above equation into the standard form.
Divide both sides by 4 in the form of
Write the 9 as
Group the denominator of the first term into a single fraction:
The foci are located at
To help you sketch the hyperbola, the center is
There is a graph of the original equation: