How do you find the foci and sketch the hyperbola #x^2/9-y^2/4=1#?
1 Answer
We know that the standard Cartesian form for the equation of a hyperbola with a transverse horizontal axis,
has foci at
If we write the given equation in the same form as equation [1], then it is a simple matter to find the foci:
Now that we have the given equation in the same form, the computation for the foci is trivial:
To graph the equation you will need the vertices:
And you will need the equations of the asymptotes:
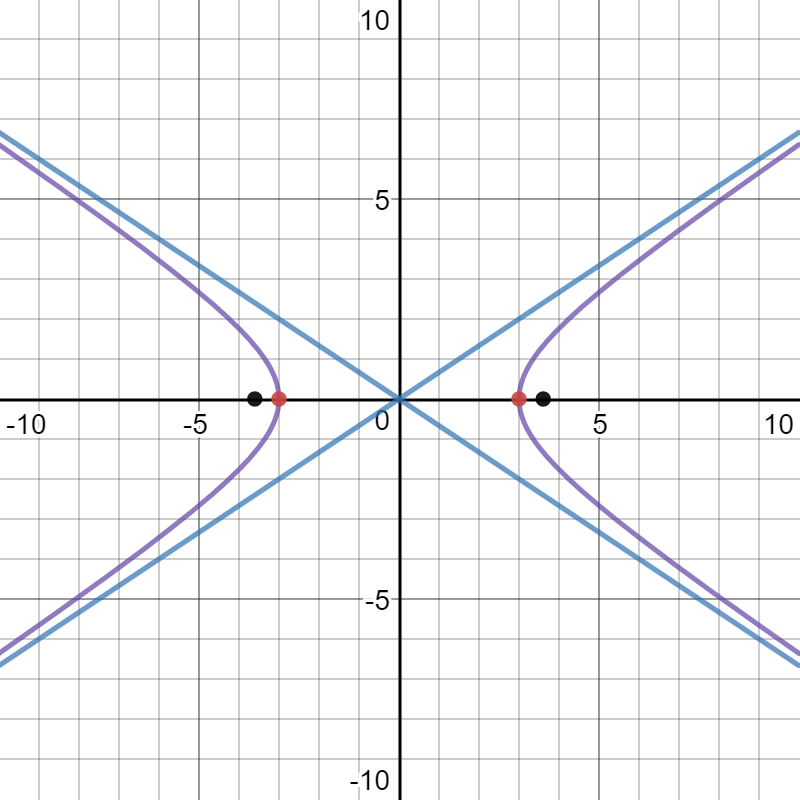
Here is a graph of, the equation, the foci, the vertices, and the asymptotes.