How do you find the general form of the equation of a circle with this equation in standard form #(-2-h)^2+(3-k)^2=25#?
1 Answer
Assuming that the intent of the given equation is that
then there is no simple standard form equation.
Explanation:
The intent of this question is not completely clear (at least to me).
I have assumed that what we are given is intended to be of the generalized form:
with given (sample) point for
with the objective of finding constants for the center
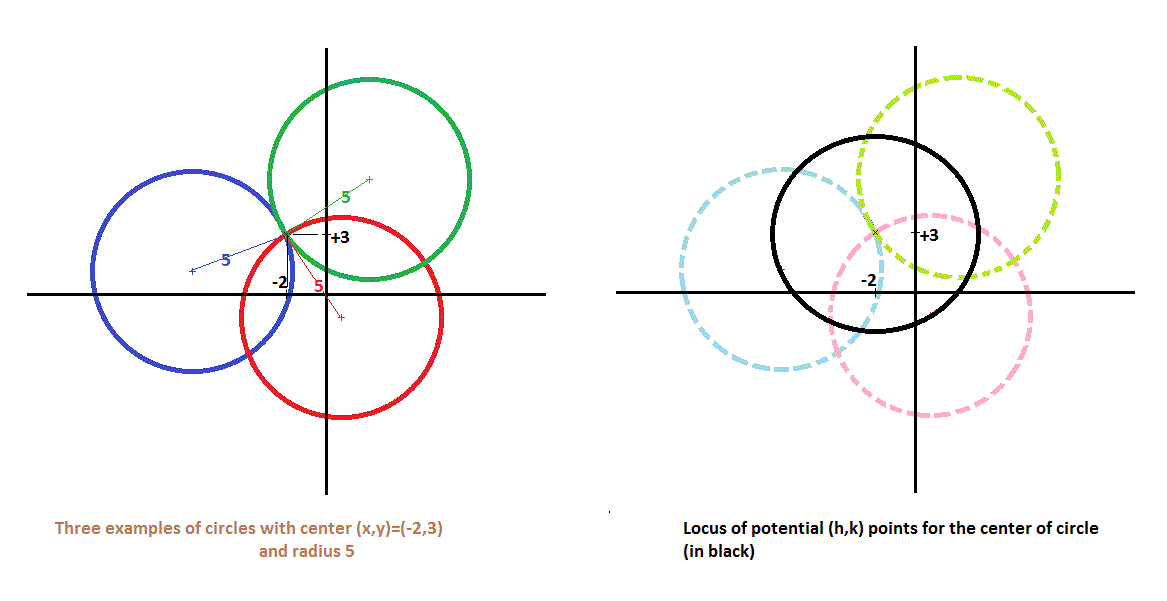
However as can been seen in the image below there are multiple (infinite number) of circles with
The collection of centers for these circles form a circle themselves at a distance of