How do you find the horizontal asymptote for #(3x^4 + 2x^2 + 1) / (5x^4 + x -1)#?
1 Answer
May 17, 2016
Explanation:
As
So
Note that for both positive and negative
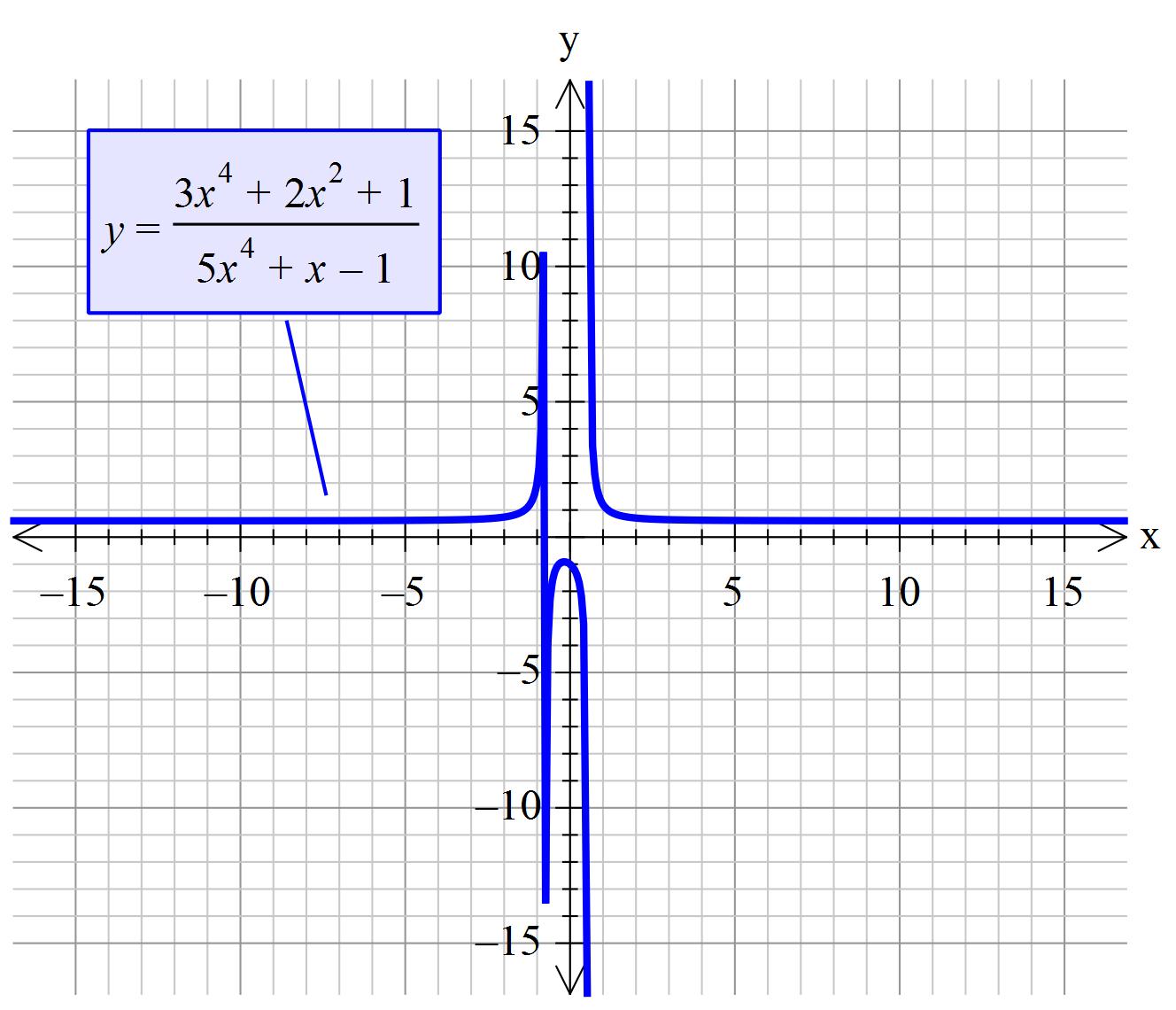
As
So
Note that for both positive and negative
