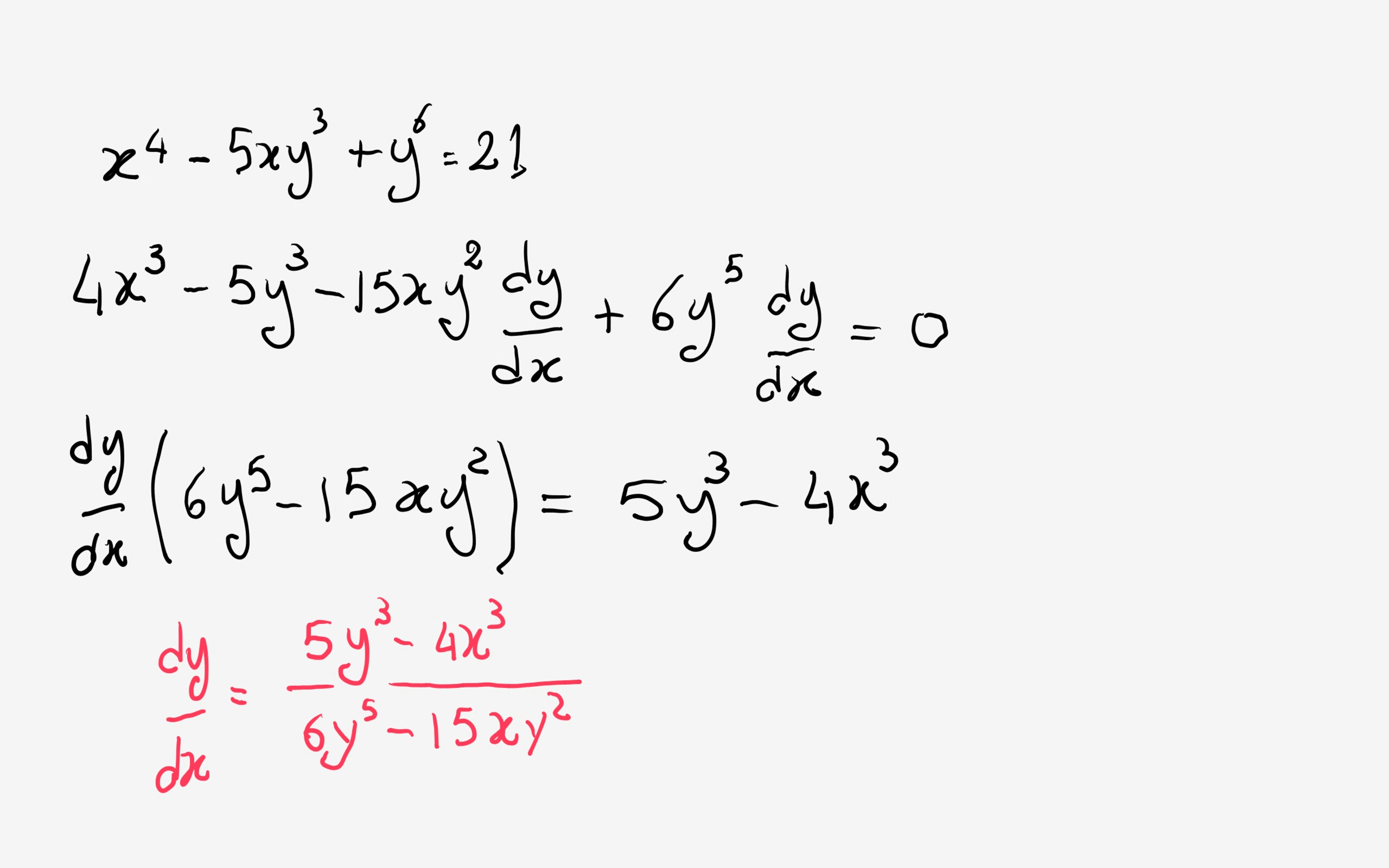Tedious, but worth it:
If #x# and #y# are related by:
#x^4-5xy^3+y^6=21#,
then we can find #y'# (or find #dy/dx)# in either of two ways.
We understand that #y# is some function (or functions) of #x#. I mean, if we choose an #x# value, we could find (or at least try to find) the value of #y# that makes the equation true.
Our choices are 1) make the funcion(s) explicit (obvious), or 2) leave the function(s) implcit (hidden) and find #y'# without first solving for #y#.
Gio has shown us how to fin #y'# without first solving for #y#, and that answers the question about implicit differentiation. I want to show the explicit function(s).
We'll solve:
#x^4-5xy^3+y^6=21#, for #y#.
#x^4-5xy^3+y^6=21#,
#y^6-5xy^3+x^4-21=0#,
This equation is quadratic in #y^3#, with #a=1#, #b=5x#, and #c=x^4-21#.
Using the quadratic formula, we get:
#y^3= (-(-5x) +- sqrt((-5x)^2-4(1)(x^4-21)))/(2(1))#
#y^3= (5x +- sqrt(25x^2-4x^4+84))/2#
So
#y=root(3)((5x +- sqrt(25x^2-4x^4+84))/2)#
Now, if we wanted to differentiate, we would get the equivalent of
#y' = dy/dx = (5y^3-4x^3)/(6y^5-15xy^2)#