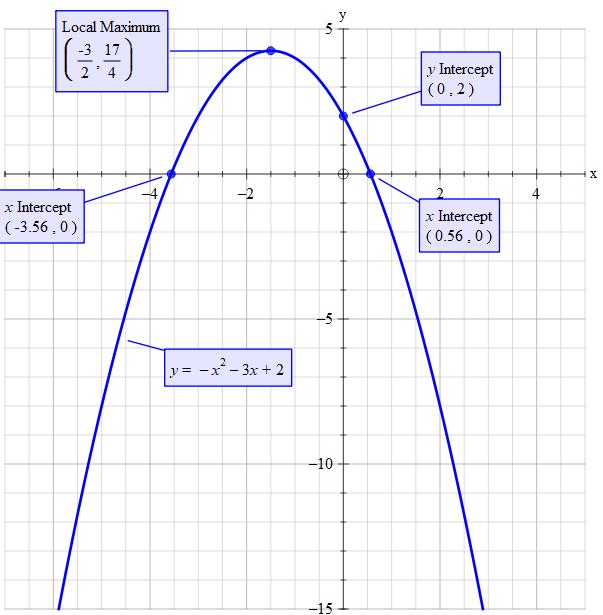
Given: #y=-x^2-3x+2#
Compare to #y=ax^2+bx+c#
As the #x^2# term in negative the general shape is #nn#
#color(red)("The y-intercept "=c=+2 ->" point" (x,y)->(0,2))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Write in the form #y=a(x^2+b/ax)+c#
In this case #a=-1 and b=-3# giving:
#y=-1(x^2+3x)+2#
#x_("vertex")=[color(white)(".")(-1/2)xx(b/a)color(white)(".")] -> [color(white)(".")(-1/2)xx(-3)/(-1)color(white)(".")] = -3/2#
So by substitution:
#y_("vertex")=-(-3/2)^2-3(-3/2)+2#
#y_("vertex")=-9/4+9/2+2 = 4 1/4->17/4#
#color(red)("Vertex"->(x,y)=(-3/2,17/4))#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Notice that #(-1)xx(-2)=+2 larr c#
and that #(-1)+(-2) = -3larr b#
so initially we would think that we have the factorisation. However the negative #x^2# gives us a problem. Perhaps we can 'force' our initial thoughts to give us the correct form.
Set #y=(x-1)(x-2)color(white)("dd") ->color(white)("dd") y=x^2-3x+2 larr" Fail"#
Lets try:
#y=(-x-1)(x-2)color(white)("dd")->color(white)("dd") y=-x^2+x+2larr" Fail"#
Ok! Looks as though we do not have whole number factorisation. So lets use the formula #x=(-b+-sqrt(b^2-4ac))/(2a)#
#y=color(white)("dd.d")ax^2+bx+c#
#y=(-1)x^2-3x+2#
So #a=-1; b=-3 and c=+2# giving:
#x=(+3+-sqrt((-3)^2-4(-1)(+2)))/(2(-1))#
#x=-3/2+-sqrt(17)/2 larr" Exact solution"#
As 17 is a prime number we can not simplify this any further.
Approximate solution:
#x=-1.5+-2.062# to 3 decimal places giving:
#color(red)(x_("intercept")~~ -3.562 and +0.562" to 3 decimal places")#