#int(x-2)/((x+1)^2+4)dx#
you can't use the integral of arctan(x) yet, because the numerator isn't just a constant. to remove the x term from the numerator, you have to use ln(x).
the formula for using ln(x) for integrals: #int(f'(x))/f(x)dx=ln(f(x))+C#
expand the denominator: #int(x-2)/(x^2+2x+5)dx#. now you want to change the numerator to be the derivative of the denominator #x^2+2x+5#. that means you want to create two fractions, one of which has the numerator #d/dx(x^2+2x+5)# or #2x+2#
rewrite #int(x-2)/(x^2+2x+5)dx# as #int(x+1-3)/(x^2+2x+5)dx = int(x+1)/(x^2+2x+5)dx - int3/(x^2+2x+5)dx = 1/2int(2x+2)/(x^2+2x+5)dx - int3/((x+1)^2+4)dx#
now the first integral has the #(f'(x))/f(x)# format and the second integral will now integrate into some form of #arctan(x)#
#1/2int(2x+2)/(x^2+2x+5)dx =1/2ln(x^2+2x+5)+C#
for # - int3/((x+1)^2+4)dx#, use the formula: 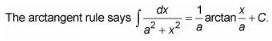
for this problem, (x+1) will equal the x in the formula, and 2 will equal the a.
#-3int1/((x+1)^2+4)dx = -3(1/2arctan((x+1)/2))+C#
combining everything:
#int(x-2)/((x+1)^2+4)dx = 1/2ln(x^2+2x+5)+C-3(1/2arctan((x+1)/2))+C#
you can merge the two C's into a single C because adding any two constants still results in a constant.
final answer: #1/2ln(x^2+2x+5)-3(1/2arctan((x+1)/2))+C#

