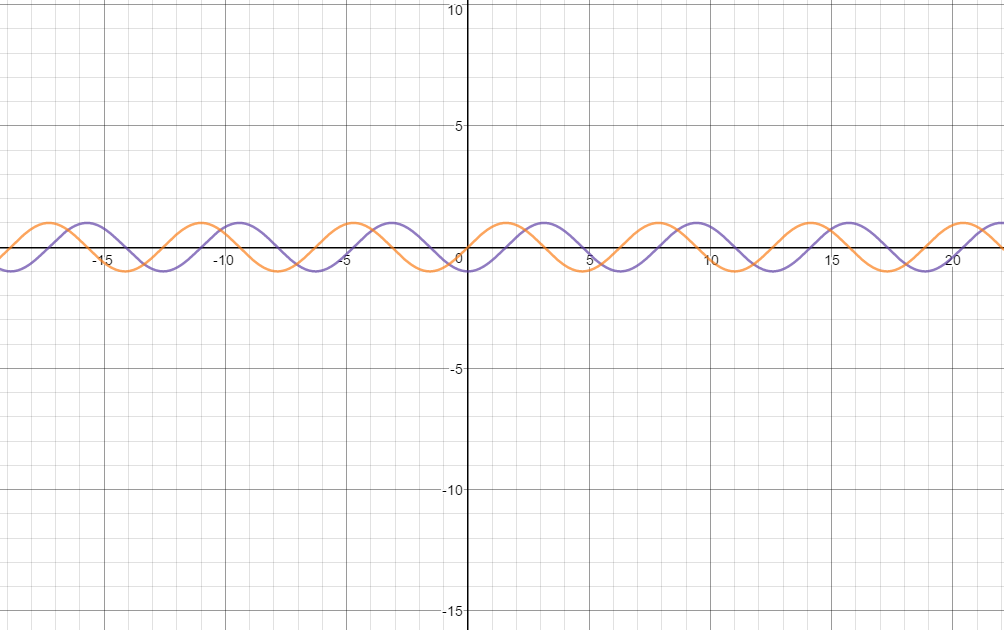
How do you find the intersections points of #y=-cosx# and #y=sinx#?
1 Answer
Nov 11, 2016
Please see the explanation.
Explanation:
Because
Divide both sides by
Use the identity
This occurs at:
where n is any integer:
The y value is
Here is a graph that shows a few intersection points: