Question

How do you find the inverse of `y = -(1/3)^x`?

Answer 1

Let `x = f^-1(x)` and then solve for `f^-1(x)`

Explanation:

Given: `f(x) = -(1/3)^x; -oo < x < oo`

Here is the graph of the function:

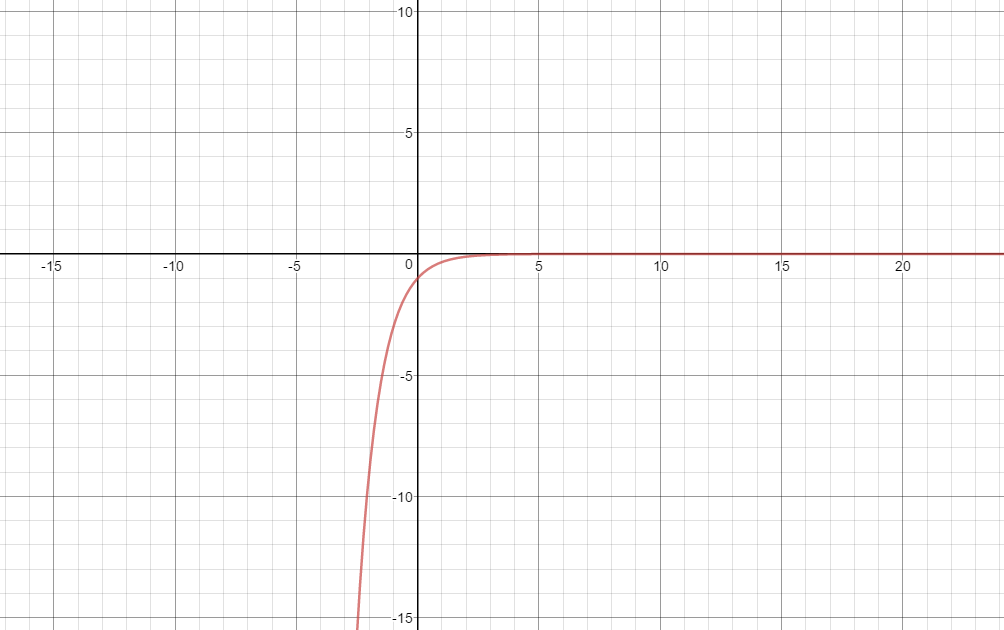
Please notice that the range of the function is `-oo < y < 0`; this will be the domain for the inverse: `-oo < x < 0`

Substitute `f^-1(x)` for every x:

`f(f^-1(x)) = -(1/3)^(f^-1(x)); -oo < x < 0`

The left side becomes x, because it is the definition of an inverse that `f(f^-1(x)) = x = f^-1(f(x))`:

`x = -(1/3)^(f^-1(x)); -oo < x < 0`

Multiply both sides by -1:

`-x = (1/3)^(f^-1(x)); -oo < x < 0`

Because x can only be negative, we can use a logarithm of undetermined base, b, on both sides:

`log_b(-x) = log_b((1/3)^(f^-1(x))); -oo < x < 0`

Use the property of logarithms `log_b(a^c) = (c)log_b(a`

`log_b(-x) = (f^-1(x))log_b(1/3); -oo < x < 0`

Use the property of logarithms `-log_b(a) = log_b(1/a)`

`log_b(-x) = (f^-1(x))(-log_b(3)); -oo < x < 0`

Divide both side by `(-log_b(3))`:

`f^-1(x) = -log_b(-x)/log_b(3); -oo < x < 0`

You can use base 10, base e, or any base that you choose.

I will leave it to you to show that `f(f^-1(x)) = x and f^-1(f(x)) = x`. You should always check this.