Question

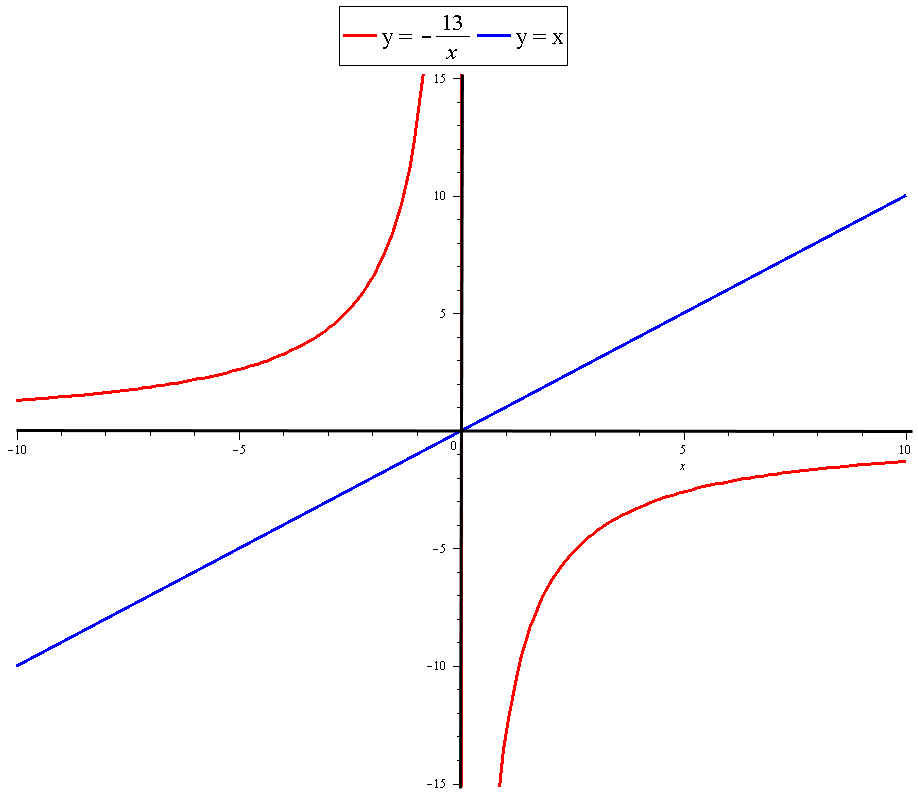
How do you find the inverse of `y = -13/x` and is it a function?

Answer 1

See below.

Explanation:

To find the inverse we need to express `bbx` as a function of `bby`:

`y=-13/x`

`xy=-13`

`x=-13/y`

Substituting `x=y`

`f^-1(x)=-13/x`

This is an example of where a function is its own inverse.

We know that if we reflect the graph of a function in the line `bb(y=x)`, we will obtain its inverse. If you observe the graph of `bb(y=-13/x)`, after reflecting it in the line `bb(y=x)` it remains unchanged.

Hence it is its own inverse.