Question

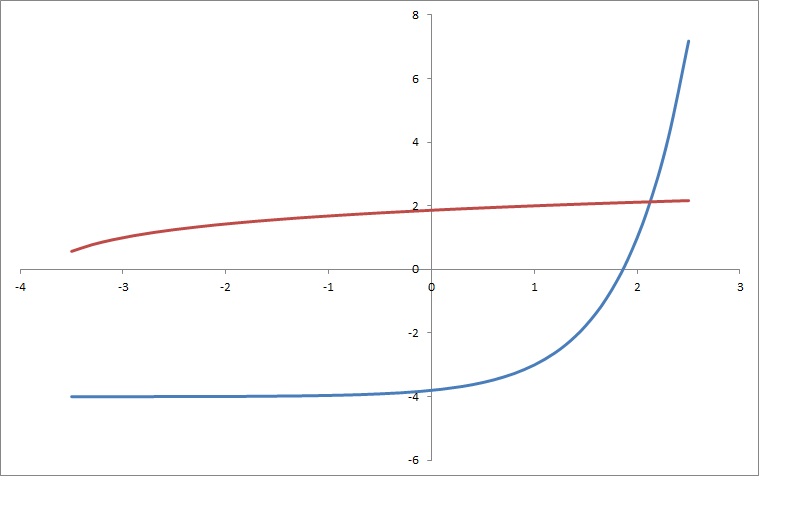
How do you find the inverse of `y=log_5(x+4)+1`?

Answer 1

I found: `y=5^(x-1)-4`

Explanation:

I would try to isolate `x` on one side by first moving `1` and then changing the log into an exponential as:
`log_5(x+4)=y-1`
`x+4=5^(y-1)`
`x=5^(y-1)-4`

Now I switch places to give it a more "friendly-function" aspect:
`y=5^(x-1)-4`

Graphically you have:
`y=log_5(x+4)+1` (red)
`y=5^(x-1)-4` (blue)