Question

How do you find the inverse of `y = - |x-3| + 5`?

Answer 1

`y=8-xcolor(white)("xxx")andcolor(white)("xxx")y=x-2`
Note that the "inverse" is not a (single-valued) function.

Explanation:

Given `y=-abs(x-3)+5`
#{: ("if",x >=3,color(white)("XXX"),"if",x < 3), (rarr,y=-(x-3)+5,,rarr,y=3-x+5), (rarr,y=x-2,,rarr,y=8-x), (rarr,x=y+2,,rarr,x=8-y), ("Noting",,,,), (,x>=3,,,x<3), (,rarr y<=5,,,y<5) :}#

Exchanging the `x` and `y` variables to give the "inverse":
#{: (color(white)("xxx"),y=x+2,color(white)("XXX"),y=8-x), ("with",,x<=5,) :}#

This makes sense if you consider the graph of `-abs(x-3)+5`

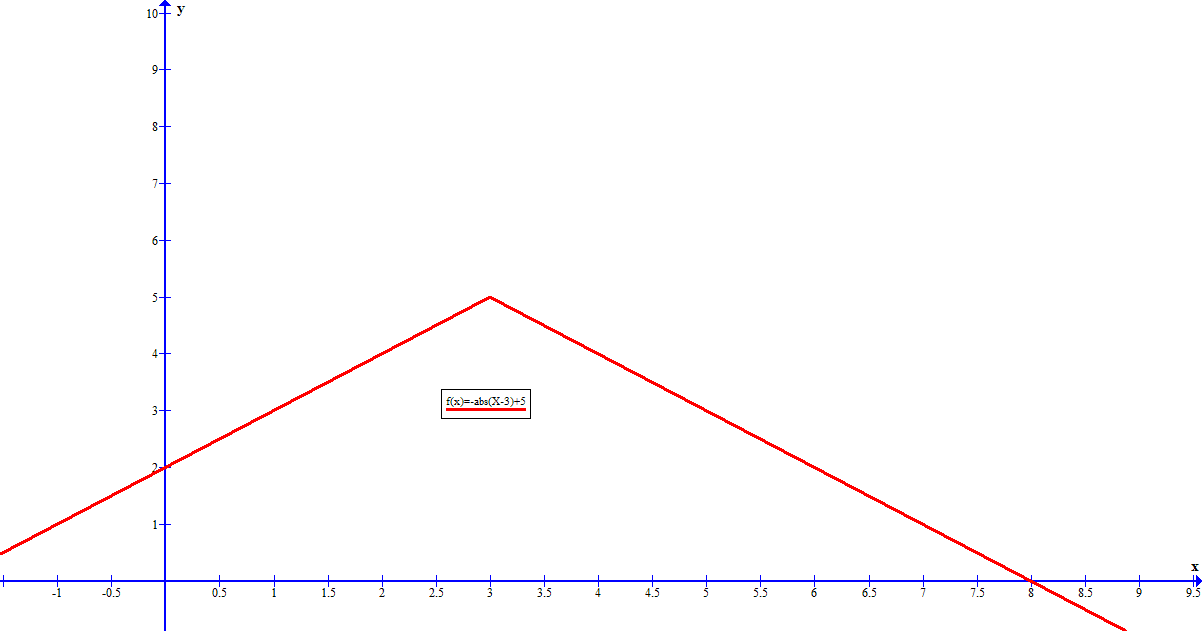
Consider any horizontal line (which will provide the inverse values).
The inverse can not have Domain values in excess of `5`
and for every value `<5`, the `2` values are provided for the Range.