How do you find the limit of (arctan(x)) / (5x) as x approaches 0?
2 Answers
Explanation:
To find this limit, notice that both the numerator and denominator go to
By applying L'Hospital's rule, we take the derivative of the numerator and denominator, giving us
We can also check this by graphing the function, to get an idea what
Graph of
graph{(arctan x)/(5x) [-0.4536, 0.482, -0.0653, 0.4025]}
A lengthier approach using trig is explained below.
Explanation:
Just in case you're not comfortable with L'Hopital's Rule, or have not yet been exposed to it, another approach to solving the problem involves using the definition of the arctangent function.
Recall that if
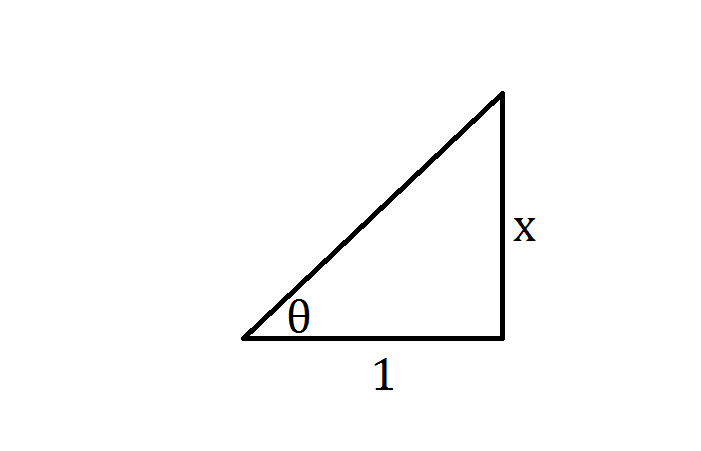
From the diagram, it is clear that
Using this plus the fact that
This is equivalent to:
We know that


