Question

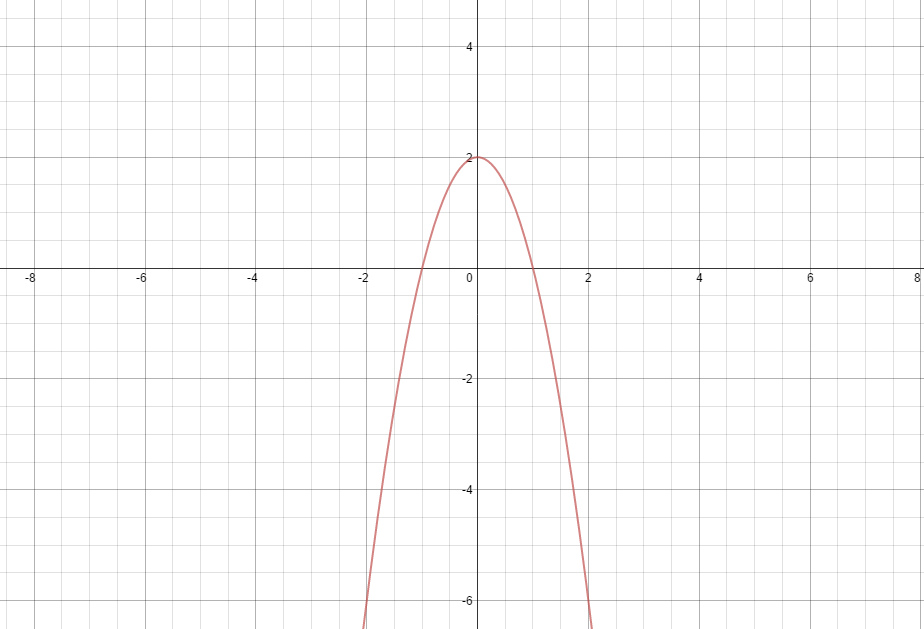
How do you find the local extrema for `f(x) = 2-2x^2` on domain `-1 <= x <= 1`?

Answer 1

It has maximum for `x=0` and value `f(0)=2` which is a absolute maximum because

`f(x)<=f(0)` for all x in `[-1,1]`

Also using derivatives we find the roots of first derivative which is

`(df(x))/dx=(d(2-2x^2))/dx=-4x`

But `(df)/dx=0=>-4x=0=>x=0`

Hence point `x=0` is a critical value of `f(x)`.Above we show that this a maximum.

The graph of `f(x)` is as follows