The Taylor series expansion of a continuous function is given as
#f(x)=f(a)+f'(a) (x-a)/(1!)+f^2(a)(x-a)^2/(2!)+f^3(a)(x-a)^3/(3!)+cdots#
or
#f(x)=sum_(n=0)^infty f^(n)(a) (x-a)^n/(n!)#
The Maclaurin series is the Taylor series expansion where #a=0#.
The best thing to do, is provide yourself a table of derivatives and those derivatives with #a=0# plugged in. Because it's a lot of derivatives, I'm going to assume you can solve the derivatives yourself.
#{:(f(x)=(1)/(1-sin(x)),f(0)=1/(1-sin(0))=1),(f'(x)=(cos(x))/(1-sin(x))^2,f'(0)=(cos(0))/(1-sin(0))^2=1),(f^2(x)=(2+sin(x))/(1-sin(x))^2,f^2(0)=2),(f^3(x)=(cos(x)(5-2sin(x)))/(1-sin(x))^3,f^3(0)=5),(f^4(x)=(cos(x)(16-6sin(x)))/(1-sin(x))^3,f^4(0)=16),(vdots,vdots):}#
It is not at all obvious what the #n^"th"# derivative or Maclaurin value is. However, we can at least plug these values into the series above and have the expansion thus far. So for #a=0#, we have
#f(x)=f(0)+f'(0) x/(1!)+f^2(0)x^2/(2!)+f^3(0)x^3/(3!)+f^4(0)x^4/(4!)+cdots#
#f(x)=1+ x/(1!)+2x^2/(2!)+5x^3/(3!)+16x^4/(4!)+cdots#
#f(x)=1+ x+x^2+5/6x^3+2/3x^4+cdots#
You can compare the two graphs and see how close they are
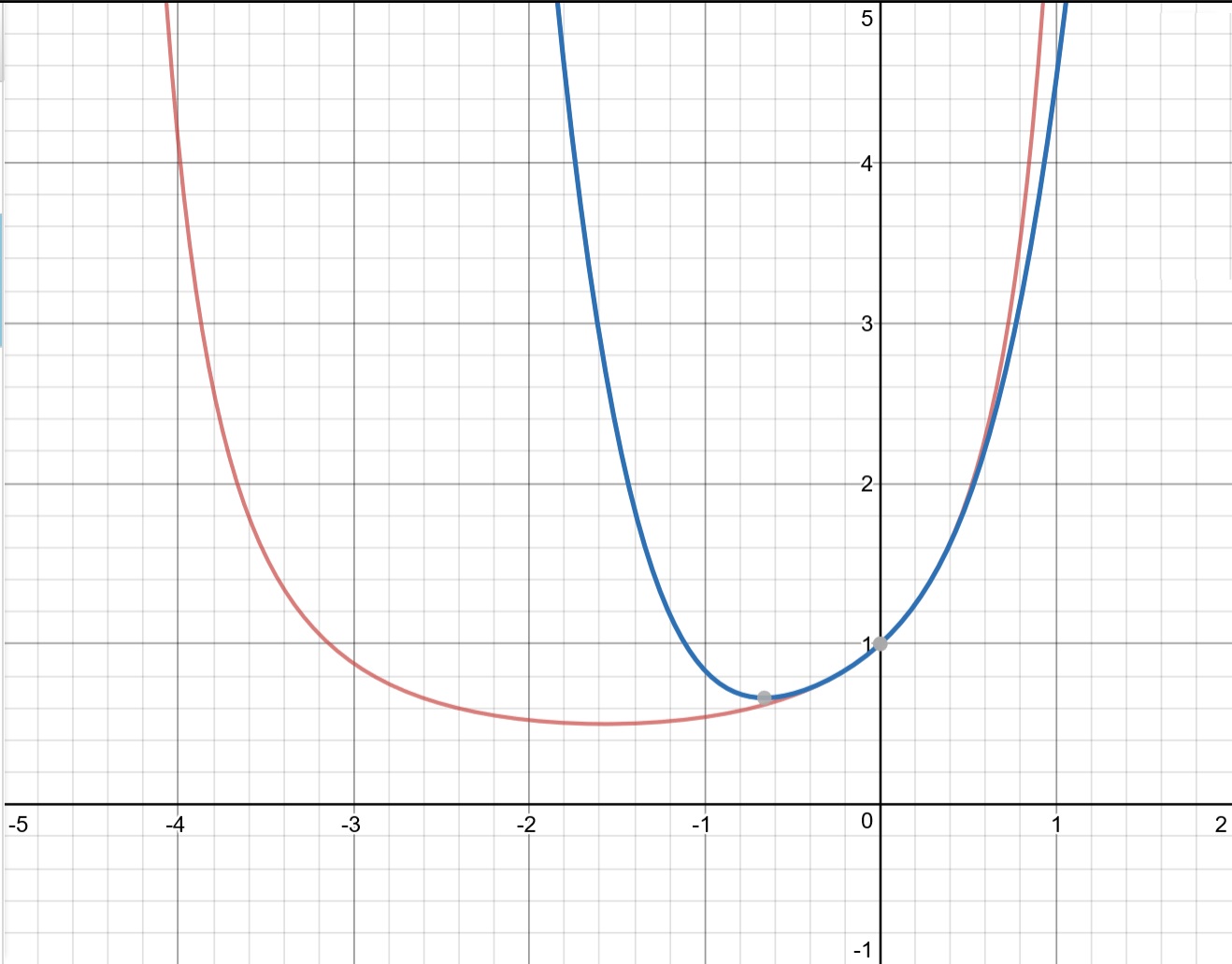
Obviously, more terms will get closer and closer.

