Question

How do you find the Maclaurin series for `ln(2-3x)`?

Answer 1

`ln 2 - 1.5 x -(1.5 x)^2/2-1.5 x)^3/3-...-(1.5 x)^n/n-...`,
`-2/3<=x<2/3`.

Explanation:

Using the Maclaurin series ln (1-X)=-X-X^2/2-X^3/3-...-X^n/n-...,#

`-1<=X<1`,

`ln(2-3x)=ln 2 + ln (1-1.5 x)`

`=ln 2 - 1.5 x -(1.5 x)^2/2-1.5 x)^3/3-...-(1.5 x)^n/n-...`,

`-1<=1.5x<1`, or explicitly, `-2/3<=x<2/3`.,

Answer 2

Let `f(x) = ln(2-3x)`, then

`f(x) = ln 2 - (3/2)^(1)/(1!) x - (3/2)^(2)/(2!) x^2 - (3/2)^(3)/(3!) x^3 - (3/2)^(4)/(4!) x^4 - ...`

`=ln2 - sum_(n=1)^(∞) (3/2)^(n)/(n!) x^n`

Explanation:

In order to find such Maclaurin series, which is just a special case of a Taylor series centered at `x=0`, we could also calculate a few derivatives and construct a series representation.

Remember that a Maclaurin series can be expressed in the following way:

`f(x) = f(0) + f^(1)(0)/(1!) x + f^(2)(0)/(2!) x^2 + f^(3)(0)/(3!) x^3 + f^(4)(0)/(4!) x^4 + ...`

`= sum_(n=0)^(∞) f^(n)(0)/(n!) x^n`

Let `f(x) = ln(2-3x) -> f(0) = ln2`

Calculating our derivatives:

`f^(1)(x) = - (3x)/(2-3x)`

`= -3(2-3x)^(-1)`

`f^(2)(x) = 3(2-3x)^(-2)(-3)`

`= -9(2-3x)^(-2)`

`f^(3)(x) =18(2-3x)^(-3)(-3)`

`= -54(2-3x)^(-3)`

`f^(4)(x) =162(2-3x)^(-4)(-3)`

`= -486(2-3x)^(-4)`

Since a Maclaurin series is centered at `x=0`, we evaluate each derivative at that point.

`f(0) = 0`

`f^(1)(0) = -3/2`

`f^(2)(0) = -9/4`

`f^(3)(0) = -54/8`

`f^(4)(0) = -486/16`

Now that we have our derivatives, we can simply substitute them into our infinite sum:

`f(x) = ln 2 - (3/2)^(1)/(1!) x - (3/2)^(2)/(2!) x^2 - (3/2)^(3)/(3!) x^3 - (3/2)^(4)/(4!) x^4 - ...`

`=ln2 - sum_(n=1)^(∞) (3/2)^(n)/(n!) x^n`

Notice that our infinite sum does not start at `n = 0` but `n =1`.

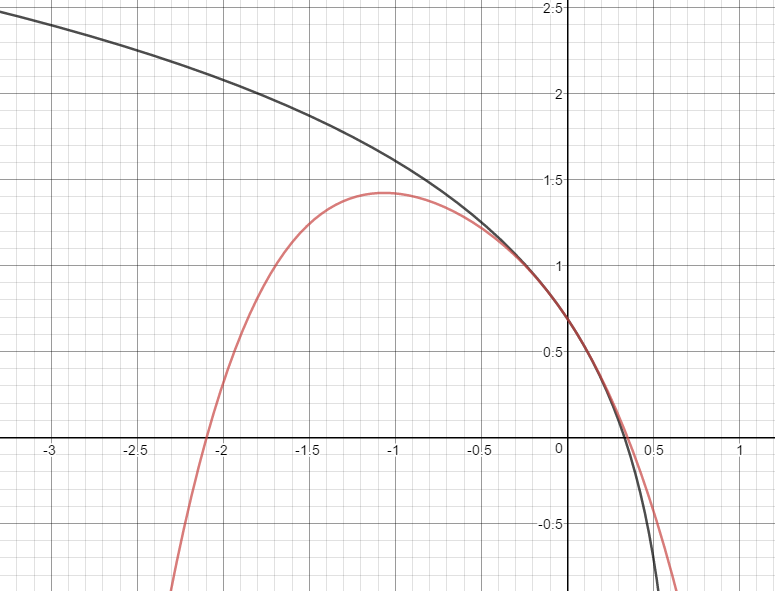
To get an idea for how this can be visualized - here are the graphs of each function (the original and the approximation).

Graph of `ln(2-3x)`

graph{ln(2-3x) [-10, 10, -5, 5]}

Graph of `ln 2 - (3/2)^(1)/(1!) x - (3/2)^(2)/(2!) x^2 - (3/2)^(3)/(3!) x^3 - (3/2)^(4)/(4!) x^4`

graph{ln 2 - (3/2)^(1)/(1!) x - (3/2)^(2)/(2!) x^2 - (3/2)^(3)/(3!) x^3 - (3/2)^(4)/(4!) x^4 [-10, 10, -5, 5]}

When both overlap, we can see that the approximation looks to be correct.