In order to find the Maclaurin series of (sin(x^2))/(x), we first need to take note of some prominent, already-derived Maclaurin series.
We know that the Maclaurin series of sin(x) is the following:
sin(x) = x-(x^3)/(3!) + (x^5)/(5!) - (x^7)/(7!) + ... = sum_(n=0)^(∞) (-1)^(n) (x^(2n+1))/((2n+1)!)
Given this known Maclaurin series, we can now see that
sin(x^2) = sum_(n=0)^(∞) (-1)^(n) ((x^2)^(2n+1))/((2n+1)!) = sum_(n=0)^(∞) (-1)^(n) (x^(4n+2))/((2n+1)!)
Note that we still have another factor we have to consider, namely the division by x, which we can easily incorporate into our series.
Since we now have the series
sin(x^2)/x = 1/x * sum_(n=0)^(∞) (-1)^(n) (x^(4n+2))/((2n+1)!)
All we need to do is to divide by an x, giving us
sum_(n=0)^(∞) (-1)^(n) (x^(4n+1))/((2n+1)!) = x/(1!) - x^(5)/(3!)+x^(9)/(5!)-x^(13)/(7!) + ...
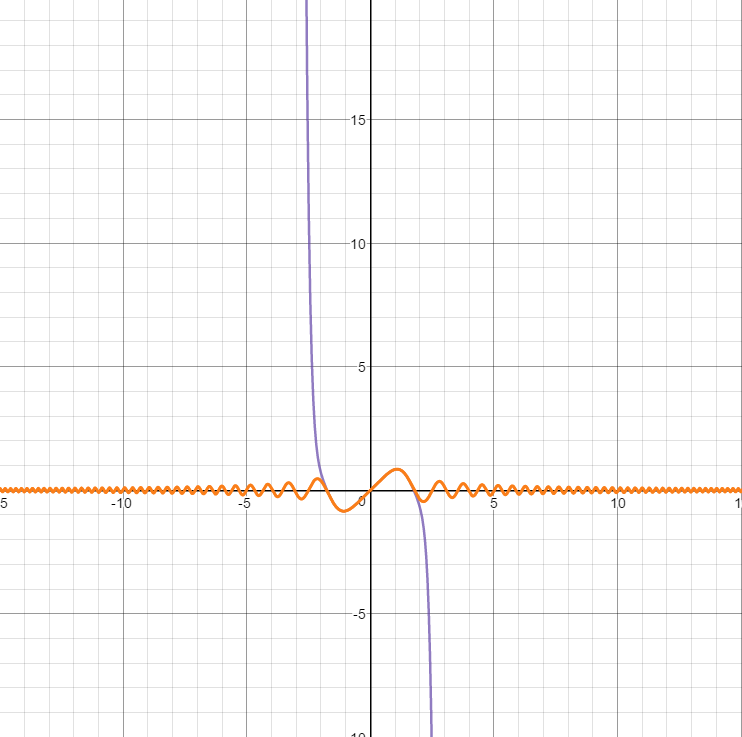
We can check the first 4 terms of this Maclaurin series, as shown in the graph below.
Graph of sin(x^2)/x
graph{sin(x^2)/x [-10, 10, -5, 5]}
Graph of x/(1!) -x^(5)/(3!)+x^(9)/(5!)-x^(13)/(7!)
graph{x-x^(5)/(3!)+x^(9)/(5!)-x^(13)/(7!) [-10, 10, -5, 5]}
Overlapping both graphs produces the following: