First we need to find the first derivative and solve this for #0#. This will identify any stationary points, because max/min points have a gradient of #0#. Inflection points can have a gradient of #0# as well, or they can have undefined gradients. ( perpendicular ).
#dy/dx(16x+x^(-2))=16-2x^(-3)=16-2/x^3#
#f'(x)=0#
#16-2/x^3=0#
#2/x^3=16#
#1/x^3=8=>x=root(3)(1/8)=1/2# for real #x#
Using second derivative, if:
#f''(x)<0# maximum point
#f''(x)>0# minimum point
#f''(x)=0# minimum/maximum or point of inflection
#f''(x)=f'(f'(x))#
#dy/dx(16-2/x^3)=6x^(-4)=6/x^4#
Plugging in #1/2#
#6/(1/2)^4>0#
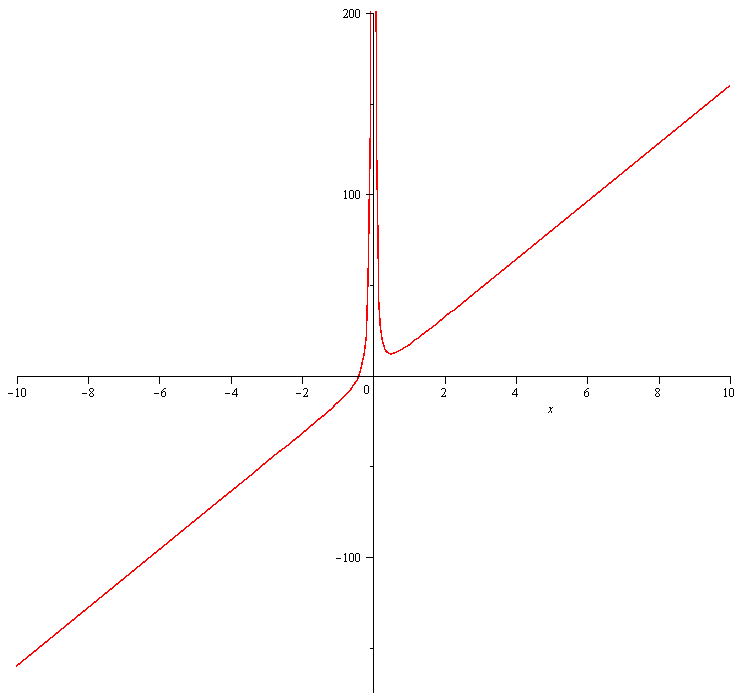
Minimum point at #(1/2 , 12)#
For concavity, if:
#f''(x)>0# convex ( concave up )
#f''(x)< 0# concave ( concave down )
#6/x^4>0#
#(-oo,0)uu(0,oo)#
Convex #(-oo,0)uu(0,oo)#
No inflection point, vertical asymptote at #x=0#
#6/x^4<0# ( no real solutions )
GRAPH: