Question

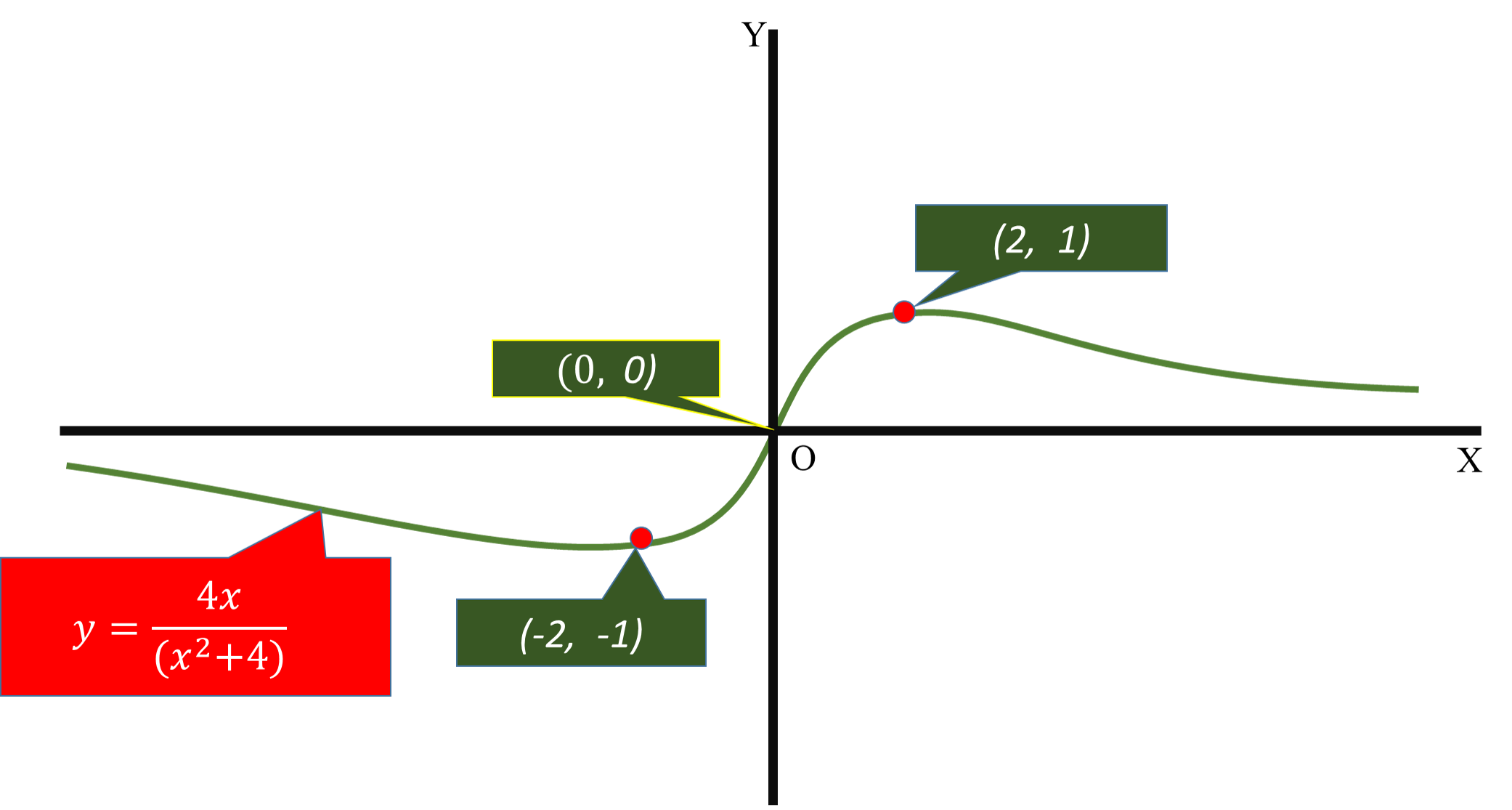
How do you find the maximum, minimum and inflection points and concavity for the function `f(x) = (4x)/(x^2+4)`?

Answer 1

`color(red)(x=2)`
`color(red)(x=-2)`

Explanation:

Given -

`f(x)=(4x)/(x^2+4)`

Find the first Derivative.

`f^'(x)={[(x^2+4)(4)]-[(4x)(2x)]}/(x^2+4)^2`

`f^'(x)=(4x^2+16-8x^2)/(x^2+4)^2`

`f^'(x)=(-4x^2+16)/(x^2+4)^2`

Find the Second Derivative

`f^''(x)={[(x^2+4)^2(-8x)]-[(-4x^2+16)(2)(x^2+4)(2x)]}/[(x^2+4)^2]^2`

`f^''(x)={[(x^2+4)^2(-8x)]-[4x(-4x^2+16)(x^2+4)]}/(x^2+4)^4`

`f^''(x)={(x^2+4)[(x^2+4)(-8x)]-[4x(-4x^2+16)]}/(x^2+4)^4`

`f^''(x)={[(x^2+4)(-8x)]-[4x(-4x^2+16)]}/(x^2+4)^3`

#f^''(x)= (-8x^3-32x+16x^3-64x)/(x^2+4)^3#

`f^''(x)=(8x^3-96x)/(x^2+4)^3`

To find the Maxima and Minima, set the 1st derivative equal to zero.

`f^'(x)=0 => (-4x^2+16)/(x^2+4)^2=0`

`-4x^2+16=0`
`x^2=(-16)/(-4)=4`
`x=+-sqrt4`

`color(red)(x=2)`
`color(red)(x=-2)`

`x` has two values

At `x=2`

`f^''(x)=(8x^3-96x)/(x^2+4)^3=[8(2)^3-96(2)]/[(2)^2+4]^3=(64-192)/1728=(-128)/1728<0`

At `x=2, f^'(x)=0; f^''<0`

Hence the function has a maximum at `x=2`

At `x=-2`

`f^''(x)=(8x^3-96x)/(x^2+4)^3=[8(-2)^3-96(-2)]/[(-2)^2+4]^3=(64+192)/1728=(256)/1728<0`

At `x=2, f^'(x)=0; f^''>0`

Hence the function has a minimum at `x=-2`