Question

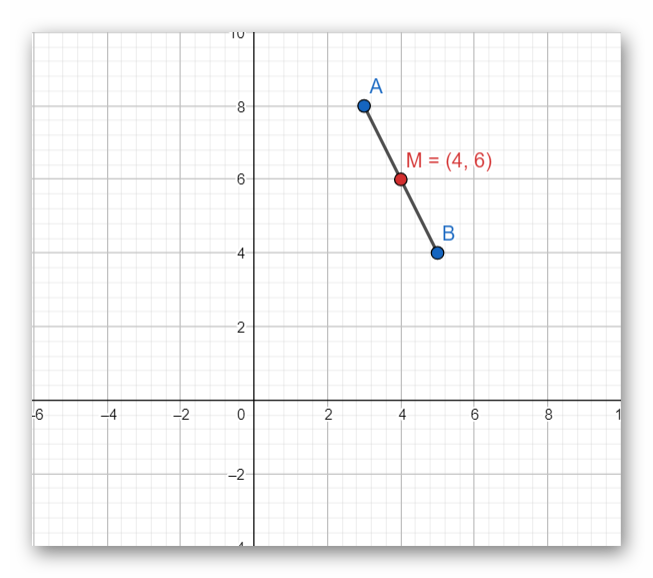
How do you find the midpoint of ( 3, 8 ) and ( 5, 4 )?

Answer 1

`(4,6)`

Explanation:

`"given coordinates of endpoints say"`

`x_1,y_1)" and "(x_2,y_2)" then"`

`"midpoint "=[1/2(x_1+x_2),1/2(y_1+y_2)]`

`"let "(x_1,y_1)=(3,8)" and "(x_2,y_2)=(5,4)`

`"midpoint "=[1/2(3+5),1/2(8+4)]`

`color(white)("midpoint ")=(4,6)`

Answer 2

The midpoint equal:
`M=(x_("midpoint"),y_("midpoint"))=(4,6)`

Explanation:

Let ;

`A=(x_1,y_1)=(3,8)`

`B=(x_2,y_2)=(5,4)`

To find the `x_("midpoint")`

`x_("midpoint")=(x_1+x_2)/2=(3+5)/2=8/2=4`

To find the `y_("midpoint")`

`y_("midpoint")=(y_1+y_2)/2=(8+4)/2=12/2=6`

The midpoint equal:

`M=(x_("midpoint"),y_("midpoint"))=(4,6)`

Show the sketch below: