How do you find the midpoint of each diagonal of the quadrilateral with vertices P(1,3), Q(6,5), R(8,0), and S(3,-2)?
1 Answer
Midpoint of the diagonal PR :
Midpoint of the diagonal QS :
Both the diagonals have the same Midpoint, and we have a Parallelogram.
Explanation:
We are given a Quadrilateral with the following Vertices:
The MidPoint Formula for a Line Segment with Vertices
Consider the Vertices
Using the Midpoint formula we can write
Consider the Vertices
Using the Midpoint formula we can write
By observing the two Intermediate results 1 and 2, we understand that both the diagonals have the same Midpoint, and hence the given Quadrilateral with four vertices is a Parallelogram.
Please refer to the image of the graph constructed using GeoGebra given below:
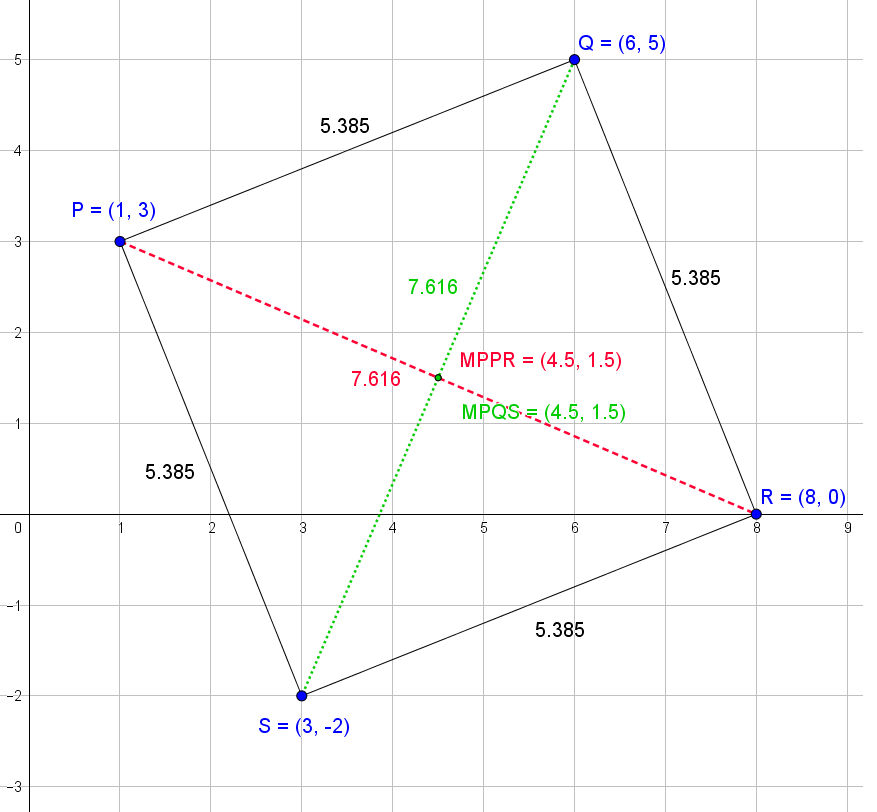
MPPR
MPQS
Some interesting properties of a parallelogram to remember:
-
Opposite sides of a parallelogram have the same length and hence they are congruent.
-
Opposite angles of the parallelogram have the same size/measure.
-
Obviously, opposite sides of a parallelogram are also parallel.
-
The diagonals of a parallelogram bisect each other.
-
Each diagonal of a parallelogram separates it into two congruent triangles.
-
We observe that our parallelogram has all sides congruent, and hence our parallelogram is a rhombus.

