How do you find the missing length of an isosceles triangle given Base = 8 Angle = 30?

1 Answer
Alan P.
Jun 16, 2015

The length of the non-base sides is #8/sqrt(3)#

Explanation:

(see diagram)
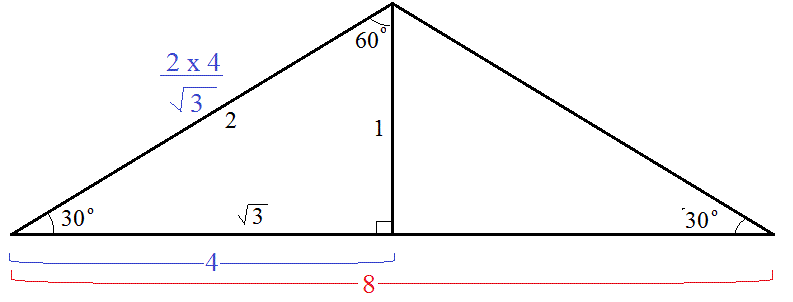
enter image source here
If the isosceles triangle is divided into two right-angled triangles, each resulting right-angled triangle has sides with well known proportions, # 2:1:sqrt(3)#
where the #sqrt(3)# proportion corresponds to the base (actually half of the base of the original isosceles triangle) and
the #2# proportion corresponds to the missing length.

#("missing length")/2 = ("half isosceles base")/sqrt(3)#

Since "half isosceles base" # = 8/2 = 4#

missing length # = (2xx4)/sqrt(3) = 8/sqrt(3)#

Related questions
See all questions in Special Right Triangles
Impact of this question
8023 views around the world
You can reuse this answer
Creative Commons License