Question

How do you find the number of complex, real and rational roots of `4x^5-5x^4+x^3-2x^2+2x-6=0`?

Answer 1

This quintic equation has one positive irrational Real zero and two complex conjugate pairs of non-Real Complex zeros.

Explanation:

Given:

`f(x) = 4x^5-5x^4+x^3-2x^2+2x-6`

`color(white)()`
Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra (FTOA) tells us that a polynomial in one variable of degree `n > 0` has a Complex (possibly Real) zero.

A straightforward corollary of the FTOA, often stated with it, is that a polynomial of degree `n > 0` has exactly `n` Complex (possibly Real) zeros, counting multiplicity.

In our example, `f(x)` is of degree `5`, so has exactly `5` Complex (possibly Real) zeros.

`color(white)()`
Descartes' Rule of Signs

The signs of `f(x)` are in the pattern: `+ - + - + -`. With `5` changes of sign, Descartes' Rule of Signs tells us that `f(x)` has `5`, `3` or `1` positive Real zero.

The signs of `f(-x)` are in the pattern `- - - - - -`. With `0` changes of sign, we can deduce that `f(x)` has no negative Real zeros.

`color(white)()`
Rational Roots Theorem

By the rational roots theorem, any rational zeros of `f(x)` are expressible in the form `p/q` for integers `p, q` with `p` a divisor of the constant term `-6` and `q` a divisor of the coefficient `4` of the leading term.

In addition, from Descartes' Rule of Signs, we know that such zeros can only be positive. So the only possible rational zeros are:

`1/4, 1/2, 3/4, 1, 3/2, 2, 3, 6`

We find:

`f(1/4) = -45/8`

`f(1/2) = -89/16`

`f(3/4) = -747/128`

`f(1) = -6`

`f(3/2) = 15/16`

`f(2) = 46`

`f(3) = 576`

`f(6) = 24774`

So `f(x)` has no rational zeros. It has an irrational Real zero somewhere in `(1, 3/2)`

`color(white)()`
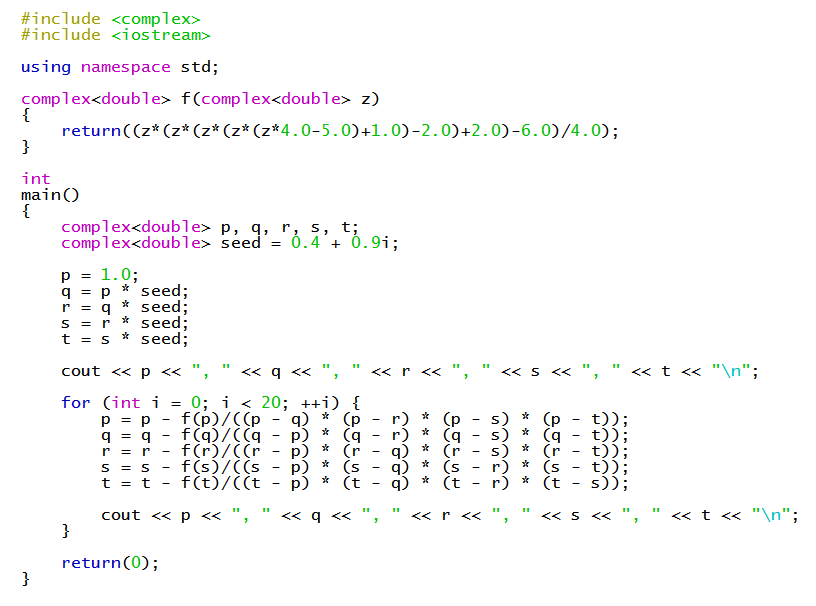
Durand-Kerner Algorithm

We can use the Durand-Kerner algorithm to find numerical approximations to the zeros.

In our example, we find approximations:

`x_1 ~~ 1.47294`

`x_(2,3) ~~ 0.547393+-0.873706i`

`x_(4,5) ~~ -0.658864+-0.723817i`

See https://socratic.org/s/aBf43swQ for another example and more information on this method.

So we find that `f(x)` has one Real and four non-Real Complex zeros.

Here's the C++ program I used to find the zeros: