Question

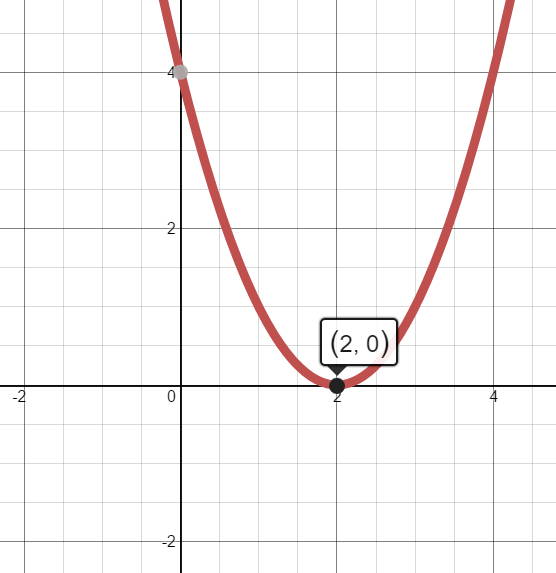
How do you find the number of roots for `x^2-4x+4` using the fundamental theorem of algebra?

Answer 1

The Fundamental Theorem of Algebra simply states for a polynomial that the total number of roots (both real and imaginary ) must equal the value of the highest exponent

Explanation:

For this problem, the highest exponent `=2`, so the Theorem states that there are two roots .

Using factoring ...

`x^2-4x+4=(x-2)(x-2)`

So, this polynomial has root `x=2` with multiplicity of 2. That simply means that 2 is a double root . Here is a sketch ...

Hope that helps