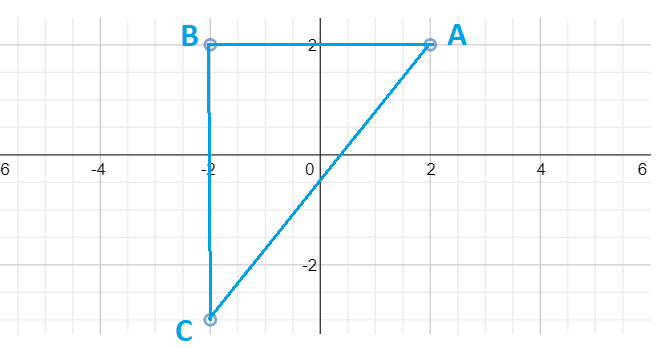
How do you find the perimeter of a triangle given (2, 2), (-2, 2), and (-2, -3)?
1 Answer
Apr 21, 2018
Perimeter is
Explanation:
To find perimeter, we should find sum of all the three sides of the triangle formed by
Before we do that observe that between
Also observe that between
As
and perimeter is