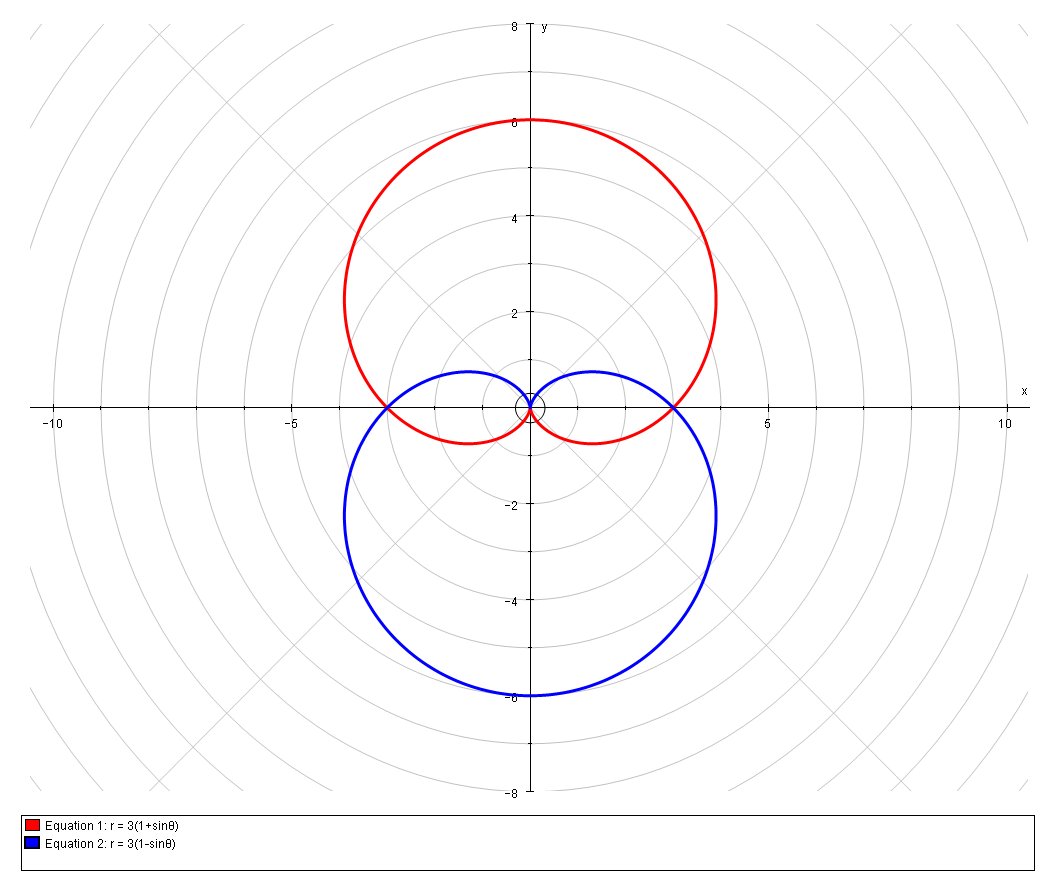
How do you find the points of intersection of #r=3(1+sintheta), r=3(1-sintheta)#?

Question

4509 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-09-03T09:41:44

Hence the points of interaction are:

# (3, sin npi) #

If we consider the interval #[0.2pi)# this gives two polar coordinates:

# (3, 0) # and # (3, pi) #

We have:

# r = 3(1+sintheta) #
# r = 3(1-sintheta) #

At any point of intersection both equations are simultaneously satisfied, so we have:

# 3(1+sintheta) = 3(1-sintheta) #
# :. 1+sintheta = 1-sintheta #
# :. 2sintheta = 0 #
# :. sintheta = 0 #
# :. theta = npi #

And with #sintheta=0# we have

# r = 3(1+0) #
# :. r =3 #

enter image source here