How do you find the polar coordinates of the point?

Question

15051 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-14T07:50:39

I am assuming that you want to convert a point in Cartesian Coordinate form to Polar Coordinate Form.

I will use an example in the explanation below.

Let us say that we want to convert a point #(0, 2)# in Cartesian Form to Polar Form.

Let us analyze the image below:

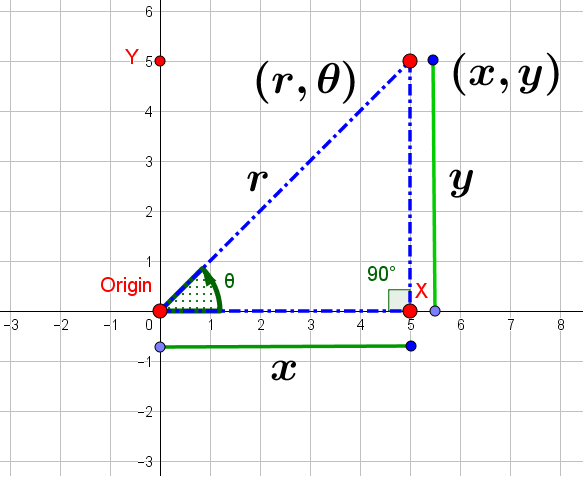
enter image source here

We have a right-triangle and hence we can use Pythagoras Theorem to define a relationship:

#x^2 + y^2 = r^2#

#tan theta = y/x#

We can see that

#cos theta = x/r#

Hence,

#color(blue)(x=r cos theta# #color(red)([ 1 ]#

#sin theta = y/r#

Hence,

#color(blue)(y = r sin theta# #color(red)([ 2 ]#

Observe that, if we are given the point #(x, y)#, then we can define #(r, theta)# and express #(x,y)# in terms of #(r cos theta, r sin theta)#.

Now, let us work on the point in Cartesian coordinate form, in our example:

#(0,2)#

Let us plot this point and look at the graph:

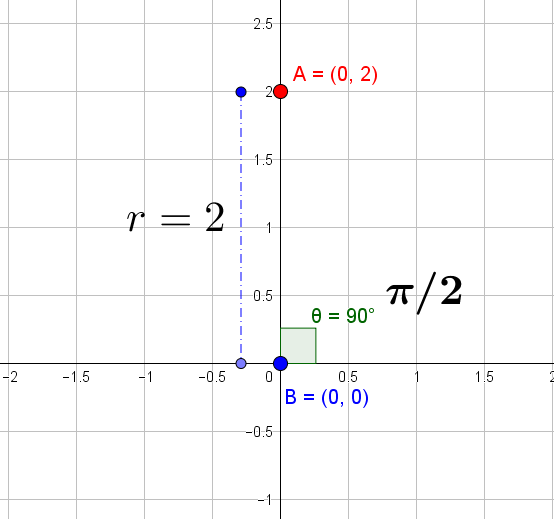
enter image source here

Now, we are in a position to convert the #(0, 2)# to equivalent Polar form using #color(red)([ 1 ]# and #color(red)([ 2 ]#

Polar form is #color(green)((r, theta)#

#rArr color(blue)((2, pi/2)#

Hope it helps.