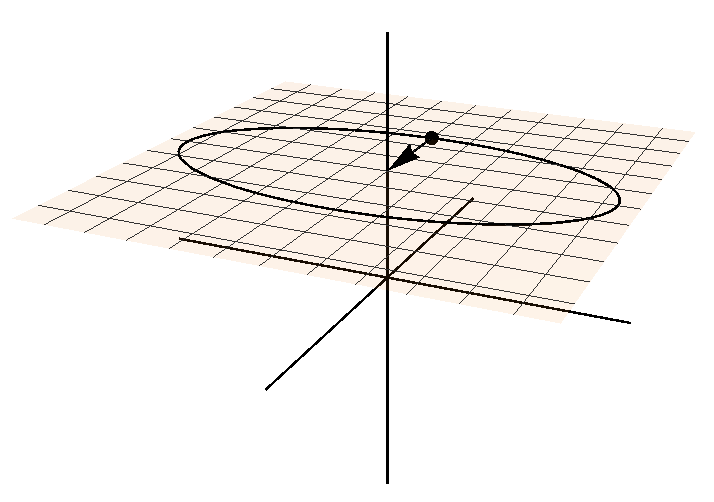
This is really a calculus problem, and the principal unit normal vector is not the same as a normal vector to the plane the curve sits in.
The velocity vector is #\vec{v}(t)=\vec{r}'(t)=-3sin(3t)\hat{i}+6cos(3t)\hat{j}# and its length (the speed) is #||\vec{v}(t)||=\sqrt{9sin^{2}(3t)+36cos^{2}(3t)}#.
This means the unit tangent vector is #\vec{T}(t)=\frac{\vec{v}(t)}{||\vec{v}(t)||}=\frac{-3sin(3t)\hat{i}+6cos(3t)\hat{j}}{\sqrt{9sin^{2}(3t)+36cos^{2}(3t)}}#. At #t=\pi#, this becomes #\vec{T}(\pi)=-\hat{j}#.
The curve lies in the plane #z=1#, so the principal unit normal vector #\vec{N}(\pi)# will lie in the same plane (and the same plane as #\vec{T}(\pi)#), it will be perpendicular to #\vec{N}(\pi)#, and it will point directly toward the center of curvature, which in this case is the center #(0,0,1)# of the ellipse that the curve is tracing out in the plane #z=1#. Also note that #r(\pi)=-\hat{i}+\hat{k}# (the curve is at the point #(-1,0,1)# at #t=\pi#).
Therefore, the principal unit normal vector will be #\vec{N}(\pi)=\hat{i}#.
Here's a picture of the situation. The positive #x#-axis is coming toward you and the positive #y#-axis is going to the right. The point #(-1,0,1)# is shown along with the unit normal vector #\vec{N}(\pi)=\hat{i}#. Again, it's not normal to the plane. It's normal to the curve and lies in the same plane as the "osculating circle" or "circle of best fit" at the given point (not shown), which lies in the plane #z=1#.