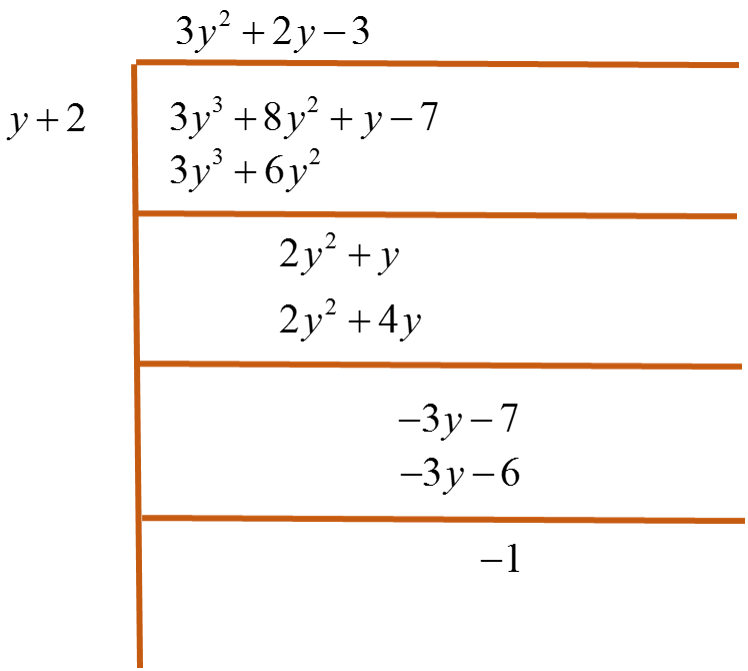
How do you find the quotient #(3y^3+8y^2+y-7)div(y+2)# using long division?

Question

2588 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2017-05-09T06:10:46

The quotient is #=3y^2+2y-3#

Let's perform the long division

#color(white)(aaaa)##3y^3+8y^2+y-7##color(white)(aaaa)##|##y+2#

#color(white)(aaaa)##3y^3+6y^2##color(white)(aaaaaaaaaaa)##|##3y^2+2y-3#

#color(white)(aaaaa)##0+2y^2+y#

#color(white)(aaaaaaa)##+2y^2+4y#

#color(white)(aaaaaaaa)##+0-3y-7#

#color(white)(aaaaaaaaaaaa)##-3y-6#

#color(white)(aaaaaaaaaaaaa)##-0-1#

The quotient is #=3y^2+2y-3# and the remainder is #=-1#

Answer 2 · 2017-05-09T06:43:48

#3y^2+2y-3#

Look at the image