Question

How do you find the roots, real and imaginary, of `y= (2x-1)^2+2 (x + 1) (x - 4)` using the quadratic formula?

Answer 1

`y = (5+sqrt(79))/6` and `(5-sqrt(79))/6`

Explanation:

First things first, we need to get this into standard form, `ax^2+bx+c`

expand

`(2x-1)(2x-1)+2(x+1)(x-4)`

distribute

`4x^2-4x-1 + (2x+2)(x-4)`

`4x^2-4x-1 + 2x^2-6x-8`

combine like-terms

`color(orange)(6)x^2 + color(blue)(-10)x + color(pink)(-9)`

The quadratic formula is `(-b)/(2a) +- ( sqrt( b^2 - 4 xx a xx c ) )/(2a)`

with `a = color(orange)(6)`, `b = color(blue)(-10)`, and `c = color(pink)(-9)`

`(-color(blue)(-10))/(2 xx color(orange)(6)) +- ( sqrt( (color(blue)(-10))^2 - 4 xx color(orange)(6) xx color(pink)(-9) ) )/(2 xx color(orange)(6))`

simplify

`10/12 +- ( sqrt( 100 + 216 ) )/(12)`

`5/6 +- (2sqrt79)/12`

`5/6 +- sqrt(79)/6`

`y = (5+sqrt(79))/6` and `(5-sqrt(79))/6`

Answer 2

`y= f(x) = (2x-1)^2+2 (x + 1) (x - 4) " "` (or)

`color(blue)(y=6x^2-10x-7`

Roots : `color(blue)(x_1 = [5-sqrt(67)]/6, " " x_2 = [5+sqrt(67)]/6 " "` (or)

`x_1 = -0.53089, or x_2 = 2.19756`

Explanation:

Given:

`y= f(x) = (2x-1)^2+2 (x + 1) (x - 4) " "` Polynomial

`color(green)(Step.1`

We will expand and simplify

`y= f(x) = (2x-1)^2+2 (x + 1) (x - 4)`

as shown below:

First, consider `color(blue)((2x-1)^2`

Using the algebraic identify,

`color(brown)((a-b)^2 -= a^2 - 2ab - b^2`,

we can expand as shown:

`rArr (2x)^2 - 2(2x)*(1) + (1)^2`

`rArr 4x^2-4x+1 " "` Expression.1

`color(green)(Step.2`

Next, consider

`color(blue)(2 (x + 1) (x - 4)`

We can factor them out to obtain

`rArr 2*(x^2 - 4x+x-4)`

`rArr 2*(x^2 - 3x-4)`

`rArr 2x^2 - 6x - 8 " "` Expression.2

`color(green)(Step.3`

We will add our Expression.1 and Expression.2 to get `y`

`(4x^2-4x+1)+(2x^2 - 6x - 8)`

`rArr 4x^2-4x+1+2x^2-6x-8`

`rArr 6x^2-10x-7`

Now, we are in a position to re-write our Polynomial as

`color(blue)(y=f(x)=6x^2-10x-7`

`color(blue)(6x^2-10x-7=0` is our Quadratic Equation,

and we proceed to find the roots.

`color(green)(Step.4`

Now that we have a Quadratic Equation in the Standard Form

`ax^2 + bx + c = 0`, where

`a = 6; b = (-10) and c = (-7)`

We now use the Quadratic Formula to find the roots

`color(red)(Root_1,_2 = -b+- sqrt(b^2-4*a*c)/(2.a)`

`rArr [-(-10)+-sqrt((-10)^2-4(6)(-7))]/(2(6)`

`rArr [10+-sqrt(100-4(-42)]]/12`

`rArr [10+-sqrt(100+168]]/12`

`rArr [10+-sqrt(268]]/12`

`rArr 10/12+-sqrt(268)/12`

`rArr 10/12+-sqrt(4*67)/12`

`rArr 10/12+-sqrt(4)/12*sqrt(67)/12`

`rArr 5/6+-2/12*sqrt(67)/12`

`rArr 5/6+-(2sqrt(67))/12`

`rArr 5/6+-(cancel 2sqrt(67))/(cancel 12( color(red)(6))`

`rArr 5/6 +-sqrt(67)/6`

`rArr (5+-sqrt(67))/6`

Hence, we can write our roots as

`color(blue)(Root_1 = [5-sqrt(67)]/6, " " Root_2 = [5+sqrt(67)]/6 " "` (or)

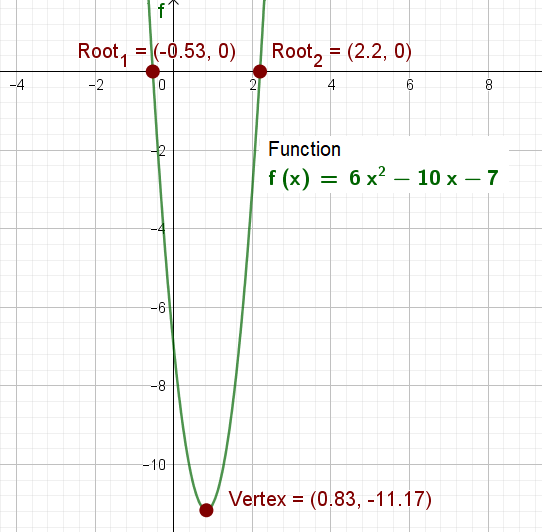
`Root_1 = -0.53089, or Root_2 = 2.19756`

Please observe that these are our required real roots, as the discriminant `color(blue)((b^2-4*a*c)>0`

`color(green)(Step.5`

We will verify our solutions using GeoGebra graphing software