You need to add like terms such that you and up with equation form:#" "y=ax^2+bx+c#
To do this expand the brackets and simplify.
'~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Expanding the brackets")#
Note that #[-(4x+3)]^2" is not the same as "-[(4x+3)^2]#
The condition we have is#" "-[(4x+3)^2]#
#color(blue)((4x+3))color(brown)((4x+3))#
#color(brown)(color(blue)(4x)(4x+3)color(blue)(+3)(4x+3)) #
#16x^2+12x" "+12x+9" "=" "color(green)(16x^2+24x+9)#
,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Substituting the expanded brackets and solving")#
#=>y=2x^2-15x-(color(green)(16x^2+24x+9))#
Multiply everything inside the brackets by -1 and group like terms
#=>y=2x^2-16x^2-15x-24x-9#
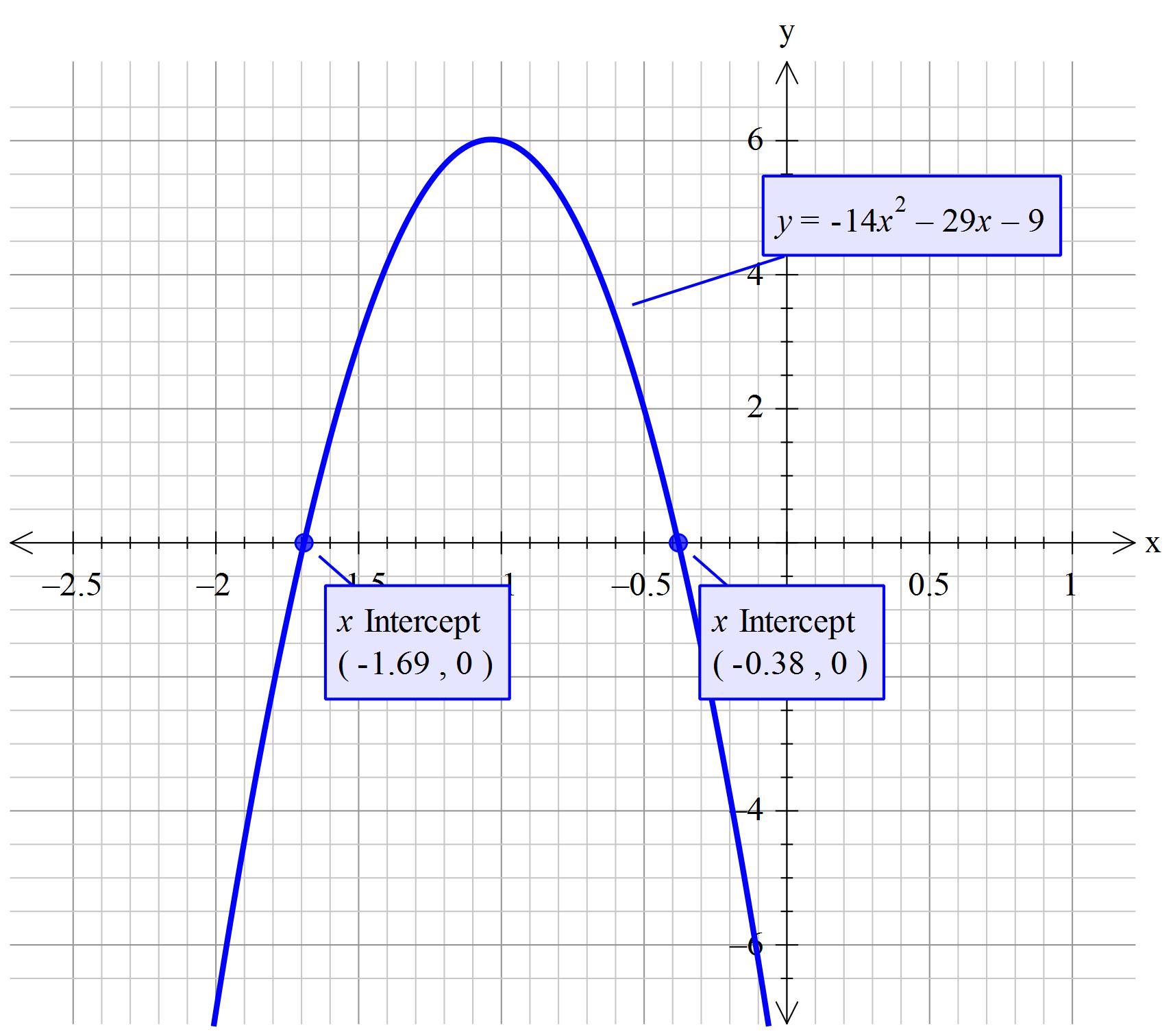
#=>y=-14x^2-29x-9#
'~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
From standard form we have:
#a=-14#
#b=-29#
#c=-9#
Thus
#x=(-b+-sqrt(b^2-4ac))/(2a) #
becomes#" "x=(+29+-sqrt((-29)^2-4(-14)(-9)))/(2(-14)#
#x=(29+-sqrt(841-504))/(-28)#
#x=(29+-sqrt(337))/(-28)" "larr 337" is a prime number"#
#color(blue)(x~~-1.69" and "x~~-0.38" to 2 decimal places")#