How do you find the roots, real and imaginary, of #y=x(x-1)-812 # using the quadratic formula?
2 Answers
The roots are at x = -28, 29.
Explanation:
Before we use the quadratic formula, we have to make the equation in standard quadratic form, or
Let's distribute the
As you can see, this is now in the form
The quadratic equation is used to find the real and imaginary roots/zeros of a quadratic equation. It's formula is
Let's plug in our values into the formula and solve for
Now simplify:
Therefore, the roots are at:
x = -28, 29
To show that this is correct, I graphed the original equation
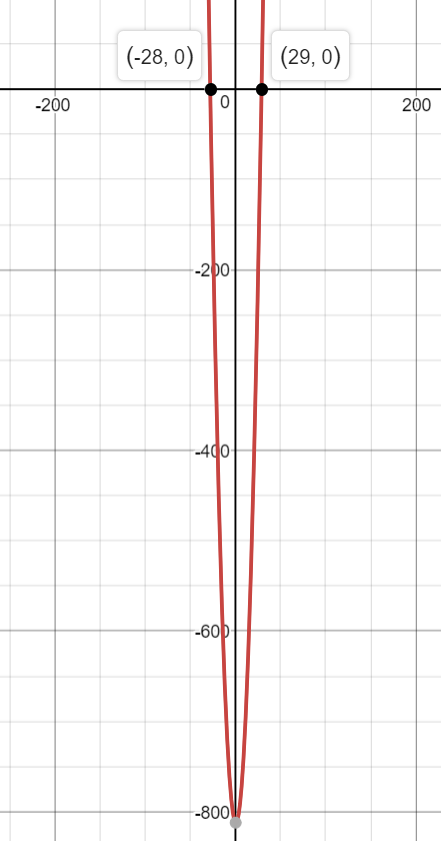
As you can see, the roots are indeed at
If you need another example, feel free to watch this Khan Academy video:
Hope this helps!
Roots are
Explanation:
Discriminant
If D is positive, only real root.
If it’s 0, it’s a perfect square.
If it’s negative, roots imaginary.
In our case, a = 1, b = -1, c = -812.
Hence, D = -1^2 - (4 * 1 * -812) = 3249#
Therefore, both roots are real.
Quadratic roots formula


