Assuming the equation #x^3+y^3=6xy-1# implicitly defines #y# as a function of #x#, we can differentiate both sides with respect to #x#, using the Power Rule, Chain Rule, and Product Rule to get:
#3x^2+3y^2*dy/dx=6y+6x*dy/dx#
Now solve this equation for #dy/dx# as follows:
#(3y^2-6x)dy/dx=6y-3x^2#
#\Rightarrow dy/dx=(6y-3x^2)/(3y^2-6x)=(2y-x^2)/(y^2-2x)#
Now differentiate this equation with respect to #x# using all the rules mentioned, as well as the Quotient Rule:
#(d^{2}y)/dx^{2}=frac{(y^2-2x)(2dy/dx-2x)-(2y-x^2)(2y*dy/dx-2)}{(y^2-2x)^2}#
#=frac{2y^2 dy/dx-2x y^2-4x dy/dx+4x^2-4y^2 dy/dx+4y+2x^2y dy/dx-2x^2}{(y^2-2x)^2}#
#=frac{(2x^2y-4x-2y^2)dy/dx+2x^2-2xy^2+4y}{(y^2-2x)^2}#
Now substitute #dy/dx=(2y-x^2)/(y^2-2x)# into this last equation to get:
#(d^{2}y)/dx^{2}=frac{(2x^2y-4x-2y^2) (2y-x^2)/(y^2-2x)+2x^2-2xy^2+4y}{(y^2-2x)^2}#
#=frac{(2x^2y-4x-2y^2) (2y-x^2)+(2x^2-2xy^2+4y)(y^2-2x)}{(y^2-2x)^3}#
This simplifies to
#(d^{2}y)/dx^{2}=frac{12x^2y^2-16xy-2x^4y-2xy^4}{(y^2-2x)^3}#
This equation would allow you to find the second derivative of this curve at any point #(x,y)# on the curve (such as #(x,y)=(0,-1)#) where you are not dividing by zero in this last equation.
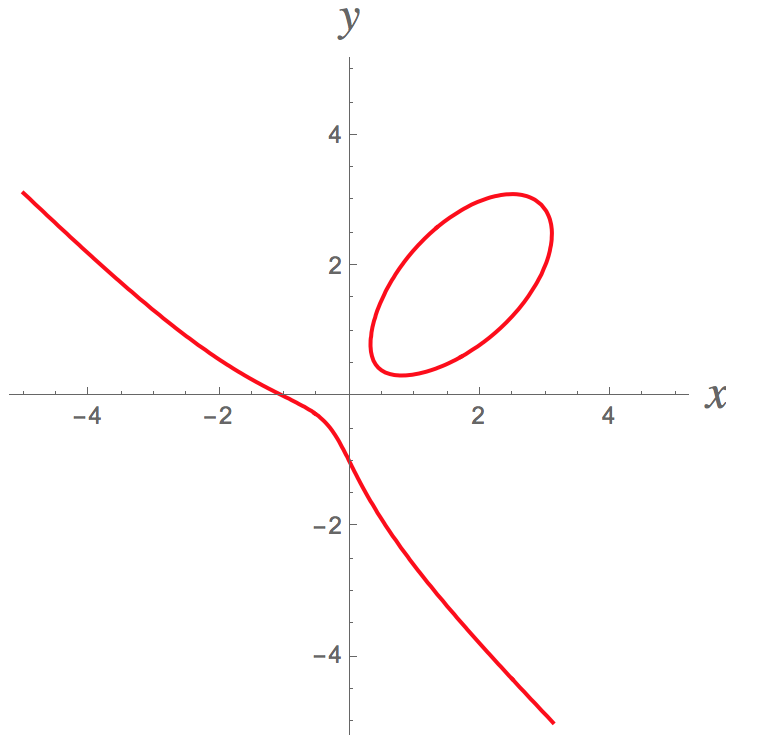
Here's a picture of the curve defined by the original equation #x^3+y^3=6xy-1#. One very interesting thing about it is that it is in two pieces!