How do you find the shape of a rectangle of maximum perimeter that can be inscribed in a circle of radius 5 cm?

Question

7806 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-04-27T15:59:49

Define the problem

Look at the figure below:

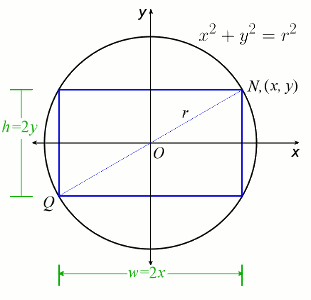
enter image source here

.

We will find the point #N(x,y)#
.

.
Perimeter, #P = 4x+4y#

In the question here, #r=5#, so we have:

#x^2 + y^2 = 25#, so

#y=sqrt(25-x^2)#

.

Therefore, the problem is:

Find #x# to maximize:

#P = 4x+4sqrt(25-x^2)#, with #0<= x <= 5#

Solution:
We find critical numbers:

#P' = 4 + (4x)/sqrt(25-x^2)#

#P'=0# at #x=-sqrt(25-x^2)#, so

#2x^2 = 25#, and so:

#x=5/sqrt2 = (5sqrt2) /2#

#P(0)=P(5)=20#

Whe #x = (5sqrt2) /2#, we also get #y = (5sqrt2) /2#, so

#P((5sqrt2) /2) = 4((5sqrt2) /2)+4((5sqrt2) /2) = 20sqrt2#

Because #20sqrt2 > 20#, the maximum value of perimeter occusu whan the rectangle is a square with sides: # (5sqrt2) /2# ,