To find the slant asymptote, we divide #x^3-4x^2+2x-5# by #x^2+2#
The resulting quotient not including the remainder part represents the slant asymptote
Let us divide
#" " " " " " " " " " " "underline(x-4" " " " " " " " " " " " " ")#
#x^2+0*x+2|~x^3-4x^2+2x-5#
#" " " " " " " " " " " "underline(x^3+0x^2+2x" " " " " " " ")#
#" " " " " " " " " " " " " "-4x^2+0-5#
#" " " " " " " " " " " " " "underline(-4x^2+0x-8" " " " " ")#
#" " " " " " " " " " " " " " " " " " " " "" " " " +3#
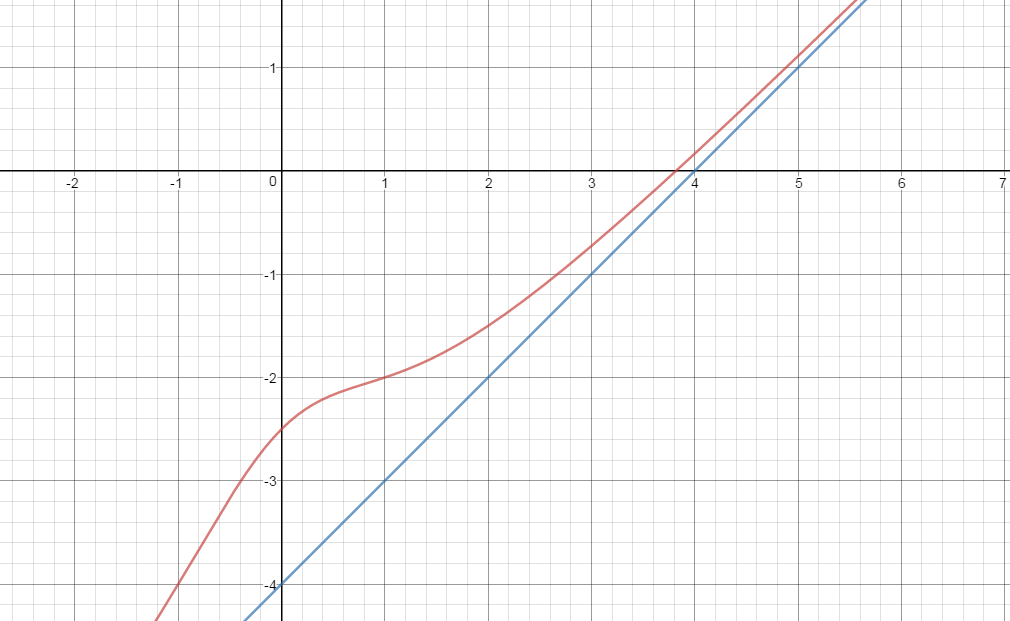
Observe the quotient #x-4# so that our slant asymptote is
#y=x-4#
Kindly see the graph of #y=(x^3-4x^2+2x-5)/(x^2+2)" "#(colored red) and the slant asymptote #y=x-4" "#(colored blue).
God bless....I hope the explanation is useful.

