If #r=f(theta)#, then #x=r cos(theta)=f(theta)cos(theta)# and #y=r sin(theta)=f(theta)sin(theta)#. This implies, by the Product Rule, that #dx/(d theta)=f'(theta)cos(theta)-f(theta)sin(theta)# and #dy/(d theta)=f'(theta)sin(theta)+f(theta)cos(theta)#.
Therefore #\mbox{slope}=dy/dx=(dy/(d theta))/(dx/(d theta))=(f'(theta)sin(theta)+f(theta)cos(theta))/(f'(theta)cos(theta)-f(theta)sin(theta))#
I tested this with the polar curve #r=f(theta)=theta#, which gave #dy/dx=(sin(theta)+theta cos(theta))/(cos(theta)-theta sin(theta))# and, at the point with polar coordinates #(r,theta)=(f(theta),theta)=(f((5pi)/6),(5pi)/6)=((5pi)/6,(5pi)/6) approx (2.62,2.62)# (and rectangular coordinates #(x,y) approx (-2.28,1.31)#)
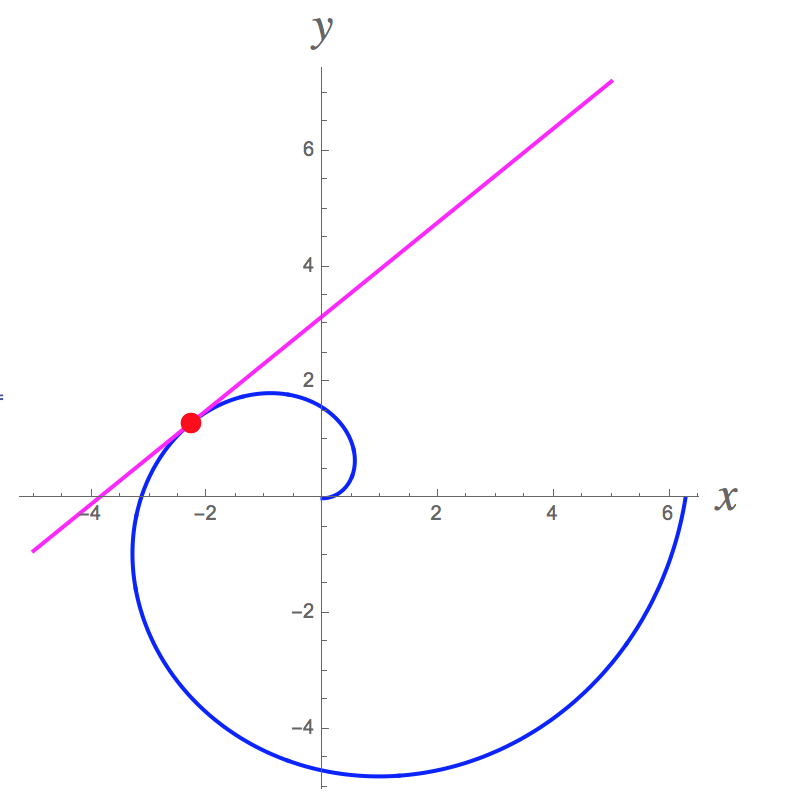
#dy/dx=(sin((5pi)/6)+(5pi)/6 * cos((5pi)/6))/(cos((5pi)/6)-(5pi)/6 * sin((5pi)/6))=(1/2 + (5pi)/6 * (-sqrt(3)/2) )/(-sqrt(3)/2 -(5pi)/6 * 1/2) approx 0.81252#. I graphed the polar curve along with its tangent at this point and got the following picture. It looks good.